In each figure alongside, a letter of the alphabet is shown along with a vertical line. Take the mirror image of the letter in the given line. Find which letters look the same after reflection (i.e. which letters look the same in the image) and which do not. Can you guess why
To solve the problem of identifying which letters of the alphabet look the same after being reflected in a vertical line (mirror image), we will analyze each letter step by step.
1. Identify the Letters: We will consider the letters A, B, O, E, M, N, P, H, L, T, S, V, and X.
2. Draw Each Letter: For each letter, we will visualize how it looks when drawn normally.
3. Draw the Vertical Line: We will draw a vertical line next to each letter to represent the mirror line.
4. Take the Mirror Image:
- For each letter, we will draw its mirror image on the opposite side of the vertical line.
5. Compare the Original and Mirror Images: We will check if the original letter and its mirror image are the same.
6. List the Results:
- Letters that look the same after reflection: A, O, M, H, T, V, X.
- Letters that do not look the same after reflection: B, E, N, P, L, S.
7. Conclusion: The letters that look the same after reflection have a vertical line of symmetry.
Detailed Analysis of Each Letter:
- A: Mirror image is the same as A.
- B: Mirror image is different from B.
- O: Mirror image is the same as O.
- E: Mirror image is different from E.
- M: Mirror image is the same as M.
- N: Mirror image is different from N.
- P: Mirror image is different from P.
- H: Mirror image is the same as H.
- L: Mirror image is different from L.
- T: Mirror image is the same as T.
- S: Mirror image is different from S.
- V: Mirror image is the same as V.
- X: Mirror image is the same as X.
Final List of Letters:
- Same After Reflection: A, O, M, H, T, V, X
- Different After Reflection: B, E, N, P, L, S
Reason for Symmetry:
The letters that look the same after reflection have a vertical line of symmetry, meaning they can be divided into two identical halves along the vertical line.
- For each letter, we will draw its mirror image on the opposite side of the vertical line.
- Letters that look the same after reflection: A, O, M, H, T, V, X.
- Letters that do not look the same after reflection: B, E, N, P, L, S.
- B: Mirror image is different from B.
- O: Mirror image is the same as O.
- E: Mirror image is different from E.
- M: Mirror image is the same as M.
- N: Mirror image is different from N.
- P: Mirror image is different from P.
- H: Mirror image is the same as H.
- L: Mirror image is different from L.
- T: Mirror image is the same as T.
- S: Mirror image is different from S.
- V: Mirror image is the same as V.
- X: Mirror image is the same as X.
- Same After Reflection: A, O, M, H, T, V, X
- Different After Reflection: B, E, N, P, L, S
The letters that look the same after reflection have a vertical line of symmetry, meaning they can be divided into two identical halves along the vertical line.
Topper's Solved these Questions
- SYMMETRYBOOK - NCERT ENGLISHCHAPTER - SYMMETRYEXERCISE - EXERCISE 13.1
5 Videos
- SYMMETRYBOOK - NCERT ENGLISHCHAPTER - SYMMETRYEXERCISE - EXERCISE 13.2
6 Videos
- RATIO AND PROPORTIONBOOK - NCERT ENGLISHCHAPTER - RATIO AND PROPORTIONEXERCISE - EXERCISE 12.1
16 Videos
- UNDERSTANDING ELEMENTARY SHAPESBOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING ELEMENTARY SHAPESEXERCISE - EXERCISE 5.5
4 Videos
Similar Questions
Which letters of the English alphabet have :
a single vertical line of symmetry
View SolutionDraw the image of the letters given below along the mirror line m.
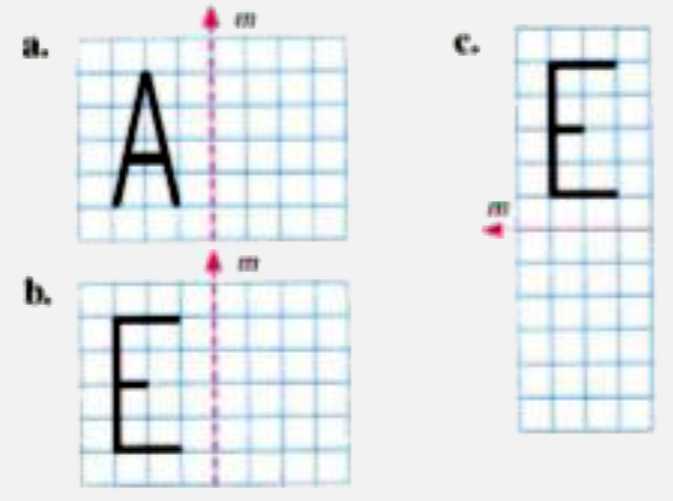 .
.
View SolutionWhich letters of the English alphabet have :
one horizontal and one vertical line of symmetry
View SolutionWhich letters of the English alphabet have :
a single horizontal line of symmetry
View SolutionDraw the reflection of the letter I along the horizontal line of symmetry shown by the dotted line in the figure does the reflection match exactly with the original image ?
 .
.
View SolutionWhich letters of the English alphabet have :
no lines of symmetry
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
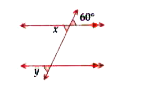
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
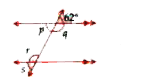
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
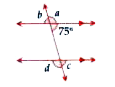
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
View Solution
