The organisers of an essay competition decide that a winner in the competition gets a prize of Rs 100 and a participant who does not win gets a prize of Rs 25. The total prize money distributed is Rs 3,000. Find the number of winners, if the total number of participants is 63.
To solve the problem step by step, we will follow the reasoning used in the video transcript.
Step 1: Define the variables
Let x be the number of winners in the competition.
Step 2: Determine the number of non-winners
Since the total number of participants is 63, the number of non-winners can be expressed as:
Number of non-winners=63−x
Step 3: Set up the equation for total prize money
The total prize money distributed is Rs 3000. The prize money for winners and non-winners can be expressed as:
- Each winner receives Rs 100, so the total prize money for winners is 100x.
- Each non-winner receives Rs 25, so the total prize money for non-winners is 25(63−x).
Combining these, we can set up the equation:
100x+25(63−x)=3000
Step 4: Simplify the equation
Now, we will simplify the equation:
100x+25×63−25x=3000
Calculating 25×63:
100x+1575−25x=3000
Combining like terms:
(100x−25x)+1575=3000
This simplifies to:
75x+1575=3000
Step 5: Isolate the variable
Next, we will isolate x by subtracting 1575 from both sides:
75x=3000−1575
Calculating the right side:
75x=1425
Step 6: Solve for x
Now, divide both sides by 75 to find x:
x=142575
Calculating the division:
x=19
Conclusion
Thus, the number of winners is:
Number of winners=19
Let x be the number of winners in the competition.
Since the total number of participants is 63, the number of non-winners can be expressed as:
Number of non-winners=63−x
The total prize money distributed is Rs 3000. The prize money for winners and non-winners can be expressed as:
- Each winner receives Rs 100, so the total prize money for winners is 100x.
- Each non-winner receives Rs 25, so the total prize money for non-winners is 25(63−x).
100x+25(63−x)=3000
Now, we will simplify the equation:
100x+25×63−25x=3000
Calculating 25×63:
100x+1575−25x=3000
Combining like terms:
(100x−25x)+1575=3000
This simplifies to:
75x+1575=3000
Next, we will isolate x by subtracting 1575 from both sides:
75x=3000−1575
Calculating the right side:
75x=1425
Now, divide both sides by 75 to find x:
x=142575
Calculating the division:
x=19
Thus, the number of winners is:
Number of winners=19
Topper's Solved these Questions
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - NCERT ENGLISHCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - EXERCISE 2.5
10 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - NCERT ENGLISHCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - SOLVED EXAMPLES
19 Videos
- INTRODUCTION TO GRAPHSBOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO GRAPHSEXERCISE - EXERCISE 15.2
4 Videos
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.4
8 Videos
Similar Questions
There are some 50 paisa and some 25 paisa coins in a ba. If the total number of coins is 30 and their total value is Rs. 11, find the number of coins of each kind.
View SolutionA cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs 90. Find the number of articles produced and the cost of each article.
View SolutionA cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs 90. Find the number of articles produced and the cost of each article.
View SolutionTwo institutions decided to award their employees for the three values of resourcefulness, competence and determination in the form of prizes at the rate of Rs x, y and z respectively per person. The first institution decided to award respectively 4, 3 and 2 employees with a total prize money of Rs 37000 and the second institution decided to award respectively 5, 3 and 4 employees with a total prize money of Rs 47000. If all the three prizes per person together amount to Rs 12000, then using matrix method find the value of x, y, and z. What values are described in this equations?
View SolutionSheela has a recurring deposit account in a bank of Rs 2,000 per month at the rate of 10% per annum. If she gets Rs 83,100 at the time of maturity, find the total time (in years) for which the account was held.
View SolutionA bag contains 25 paise and 50 paise coins whose total value is Rs30. If the number of 25 paise coins is four times that of 50 paise coins, find the number of each type of coins.
View SolutionVijay had some bananas and he divided them into two lots A and B. He sold the first lot at the rate of RS. 2 for 3 bananas and the second lot at the rate of Rs 1 per banana and got a total of Rs. 400. If he had sold the first lot at the rate of Rs. 1 per banana and the second lot at the rate of Rs.4 for 5 bananas , his total collection would have been Rs 460. Find the total number of bananas he had.
View SolutionA daily wage worker works for 23 days in a month. He gets Rs 400 per working day. However, his supervisor is very strict and fines him Rs 100 for each day he arrives late to work. If at the end of the 23 days, the worker has earned Rs 8000, find out the number of days he reached for work on time and the number of days he was late.
View SolutionA manufacturer manufactures two types of tea-cups, A and B. Three machines are needed for manufacturing the tea cups. The time in minutes required for manufacturing each cup on the machines is given below:
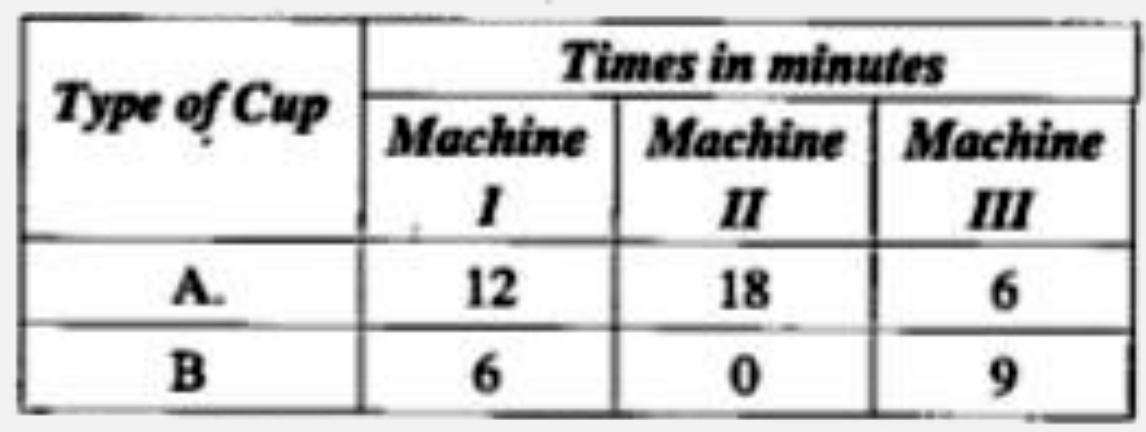
Each machine is available for a maximum of six hours per day. If the profit on each cup of type A is Rs 1.50and that'on each cup of type B is Rs 1.00, find the number of cups of each type that should be manufactured in a day to get maximumprofit.
View SolutionTwo factories decided to award their employees for three values of (a) adaptable to new techniques, (b) careful and alert in difficult situations and (c) keeping calm in tense situations, at the rate of Rs x, y and z per person respectively. The first factory decided to honour respectively 2, 4 and 3 employees with a total prize money of Rs 29000. The second factory decided to honour respectively 5, 2 and 3 employees with the prize money of Rs 30500. If the three prizes per person together cost Rs 9500, then represent the above situation by a matrix equation and form linear equations using matrix multiplication. Solve these equations using matrices. (iii) Which values are reflected in the questions?
View Solution
