Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
To find the area of the octagonal surface of the raised platform, we can break the problem down into manageable steps. Here’s a step-by-step solution:
Step 1: Understand the Shape
The top surface of the raised platform is a regular octagon. A regular octagon has eight equal sides and equal angles.
Step 2: Identify the Dimensions
From the problem, we know:
- Each side of the octagon (ab, bc, cd, etc.) is 5 meters.
- The distance across the octagon (ac) is 11 meters.
- The height of the trapezium (the distance between the parallel sides) is 4 meters.
Step 3: Calculate the Area of the Trapezium
The area of a trapezium can be calculated using the formula:
Area=12×(Base1+Base2)×Height
For trapezium ABCH:
- Base 1 (AB) = 5 meters
- Base 2 (CH) = 11 meters
- Height = 4 meters
Substituting the values into the formula:
AreaABCH=12×(5+11)×4=12×16×4=32m2
Step 4: Calculate the Area of the Rectangle
The area of a rectangle can be calculated using the formula:
Area=Length×Breadth
For rectangle HCDG:
- Length (HC) = 11 meters
- Breadth (CD) = 5 meters
Substituting the values into the formula:
AreaHCDG=11×5=55m2
Step 5: Calculate the Total Area of the Octagon
The total area of the octagonal surface can be found by adding the areas of the trapezium and the rectangle, and then multiplying by 2 (since there are two trapeziums):
Total Area=2×AreaABCH+AreaHCDG
Substituting the values:
Total Area=2×32+55=64+55=119m2
Final Answer
The area of the octagonal surface is 119m2.
---
The top surface of the raised platform is a regular octagon. A regular octagon has eight equal sides and equal angles.
From the problem, we know:
- Each side of the octagon (ab, bc, cd, etc.) is 5 meters.
- The distance across the octagon (ac) is 11 meters.
- The height of the trapezium (the distance between the parallel sides) is 4 meters.
The area of a trapezium can be calculated using the formula:
Area=12×(Base1+Base2)×Height
For trapezium ABCH:
- Base 1 (AB) = 5 meters
- Base 2 (CH) = 11 meters
- Height = 4 meters
AreaABCH=12×(5+11)×4=12×16×4=32m2
The area of a rectangle can be calculated using the formula:
Area=Length×Breadth
For rectangle HCDG:
- Length (HC) = 11 meters
- Breadth (CD) = 5 meters
AreaHCDG=11×5=55m2
The total area of the octagonal surface can be found by adding the areas of the trapezium and the rectangle, and then multiplying by 2 (since there are two trapeziums):
Total Area=2×AreaABCH+AreaHCDG
Substituting the values:
Total Area=2×32+55=64+55=119m2
The area of the octagonal surface is 119m2.
Topper's Solved these Questions
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.1
5 Videos
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - SOLVED EXAMPLES
11 Videos
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.4
8 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - NCERT ENGLISHCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - EXERCISE 2.3
9 Videos
- PLAYING WITH NUMBERSBOOK - NCERT ENGLISHCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 16.1
10 Videos
Similar Questions
Knowledge Check

Johan recieves an order for a carpet in the shape of a regular octagon with 8 inche sides. The octangonal carpet will be cut out from a square piece of carpet , as shown in the figure above. What is the area of the one of the 4 congruent triangles that will be cut out from the square?A16B16√2C16√3D64The measure of the sum of the interior angles of a regular n-sided polygon is (n-2)180∘. A regular octagon is shown below. What is the measure of the designated angle ?
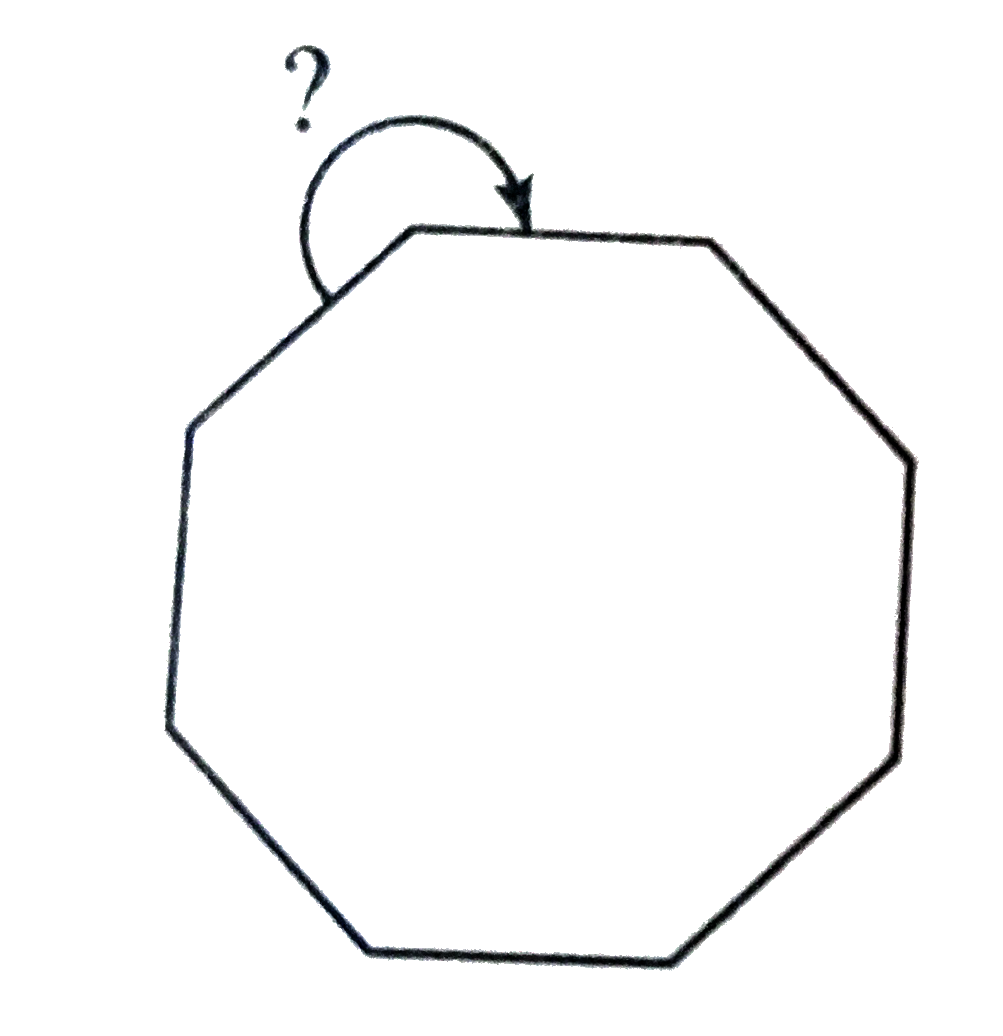 A135∘B144∘C200∘D225∘
A135∘B144∘C200∘D225∘
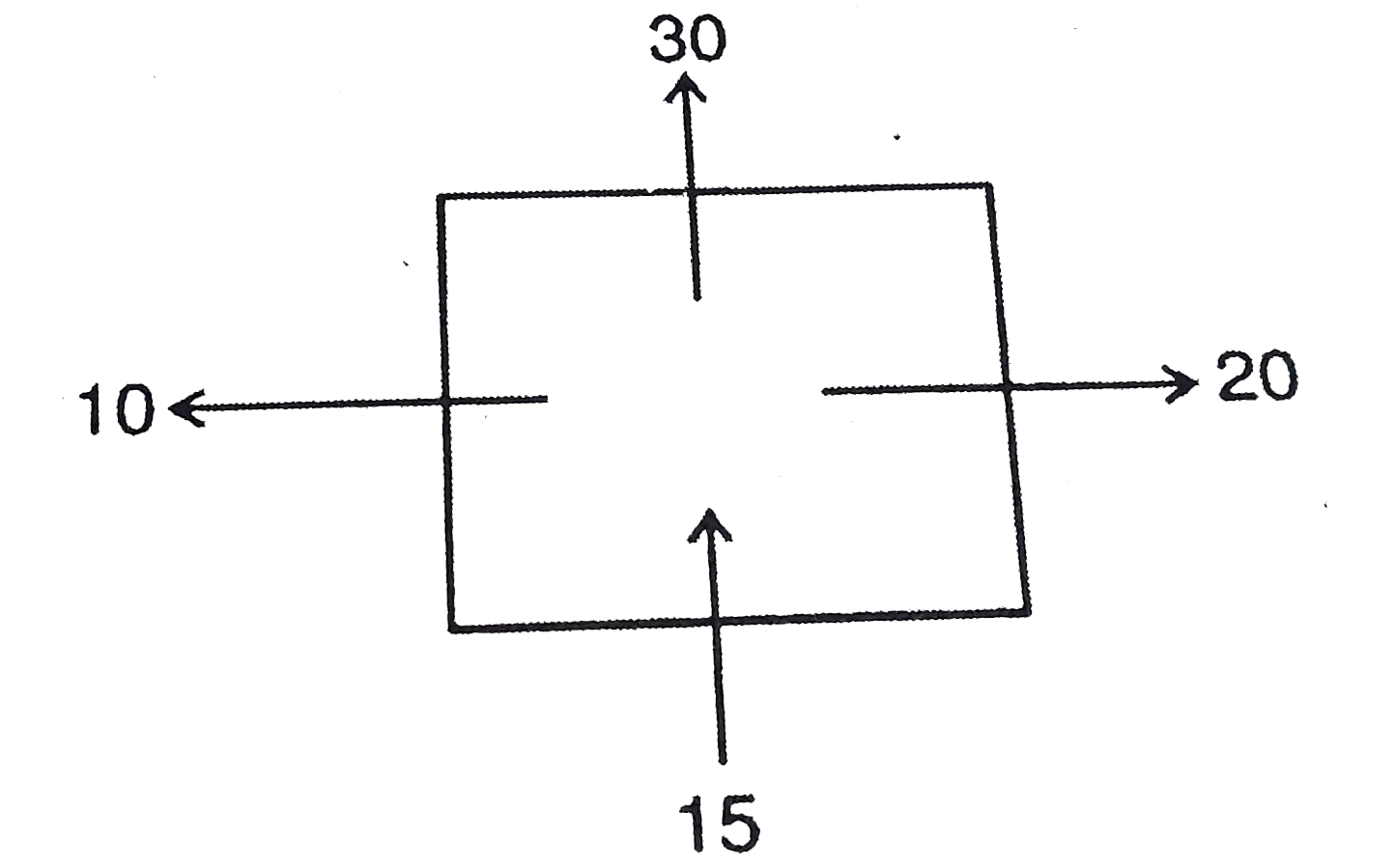
Flux (in S.I. units) coming out and eantering a closed surface is shown in the figure. Find charge enclosed by the closed surface.
View SolutionFind the perimeter of the following:
A regular octagon with each side 9 cm
View SolutionExpress in circular measure and also in degrees the angle of a regular octagon.
View SolutionIn a octagon, four of the angles are equal and each of the others is 20° more than each of the first four. Find the angles of the octagon.
View SolutionFind the area of the following regular hexagon Figure
View SolutionThe curved surface area of a cylinder is twice the sum of areas of its two end surfaces. Find the ratio of its heigth and radius.
View Solution
