A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. In the following table, find the parts of base that need to be added. Parts of red pigment 1,4,7,12,20 Parts of base 8..........
To solve the problem, we need to find the parts of base that need to be added for different amounts of red pigment while maintaining the ratio of 1 part of red pigment to 8 parts of base.
1. Understanding the Ratio:
The ratio of red pigment to base is given as 1:8. This means for every 1 part of red pigment, there are 8 parts of base.
2. Setting Up the Table:
We will create a table with two columns: one for the parts of red pigment and the other for the corresponding parts of base.
| Parts of Red Pigment | Parts of Base |
|----------------------|----------------|
| 1 | 8 |
| 4 | ? |
| 7 | ? |
| 12 | ? |
| 20 | ? |
3. Finding Parts of Base for Each Amount of Red Pigment:
We will use the ratio to find the missing values in the base column.
- For 4 parts of red pigment:
Base=Red Pigment×8=4×8=32
- For 7 parts of red pigment:
Base=Red Pigment×8=7×8=56
- For 12 parts of red pigment:
Base=Red Pigment×8=12×8=96
- For 20 parts of red pigment:
Base=Red Pigment×8=20×8=160
4. Final Table:
Now we can fill in the table with the calculated values.
| Parts of Red Pigment | Parts of Base |
|----------------------|----------------|
| 1 | 8 |
| 4 | 32 |
| 7 | 56 |
| 12 | 96 |
| 20 | 160 |
Summary of Results:
- For 1 part of red pigment, 8 parts of base are needed.
- For 4 parts of red pigment, 32 parts of base are needed.
- For 7 parts of red pigment, 56 parts of base are needed.
- For 12 parts of red pigment, 96 parts of base are needed.
- For 20 parts of red pigment, 160 parts of base are needed.
The ratio of red pigment to base is given as 1:8. This means for every 1 part of red pigment, there are 8 parts of base.
We will create a table with two columns: one for the parts of red pigment and the other for the corresponding parts of base.
|----------------------|----------------|
| 1 | 8 |
| 4 | ? |
| 7 | ? |
| 12 | ? |
| 20 | ? |
We will use the ratio to find the missing values in the base column.
Base=Red Pigment×8=4×8=32
Base=Red Pigment×8=7×8=56
Base=Red Pigment×8=12×8=96
Base=Red Pigment×8=20×8=160
Now we can fill in the table with the calculated values.
|----------------------|----------------|
| 1 | 8 |
| 4 | 32 |
| 7 | 56 |
| 12 | 96 |
| 20 | 160 |
- For 1 part of red pigment, 8 parts of base are needed.
- For 4 parts of red pigment, 32 parts of base are needed.
- For 7 parts of red pigment, 56 parts of base are needed.
- For 12 parts of red pigment, 96 parts of base are needed.
- For 20 parts of red pigment, 160 parts of base are needed.
Topper's Solved these Questions
- DIRECT AND INVERSE PROPORTIONSBOOK - NCERT ENGLISHCHAPTER - DIRECT AND INVERSE PROPORTIONSEXERCISE - SOLVED EXAMPLES
8 Videos
- DATA HANDLINGBOOK - NCERT ENGLISHCHAPTER - DATA HANDLINGEXERCISE - SOLVED EXAMPLES
1 Videos
- EXPONENTS AND POWERSBOOK - NCERT ENGLISHCHAPTER - EXPONENTS AND POWERSEXERCISE - SOLVED EXAMPLES
9 Videos
Similar Questions
if 1 part of a red pigment requires 75 mL of base, how much red pigment should we mix with 1800 mL of base?
View SolutionAn endoscope is employed by a physician to view the internal parts of body organ. It is based on the principle of
View SolutionAn endoscope is employed by a physician to view the internal parts of body organ. It is based on the principle of
View SolutionStudy the diagram and answer the questions that follow :
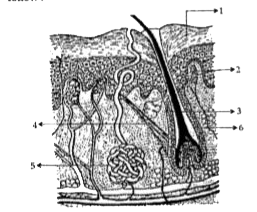
Label the parts 1 - 4.
View SolutionStudy the diagram and answer the questions that follow :

Label the parts 1 - 4.
View SolutionA pack of 52 cards is divided at random into two equals parts. Find the probability that both parts will have an equal number of black and red cards.
View SolutionFind the real part of (1−i)−i.
View SolutionFind the real part of (1−i)−i.
View SolutionStudy the diagram and answer the questions that follow :
Label the parts 1 - 4
View SolutionStudy the diagram and answer the questions that follow:
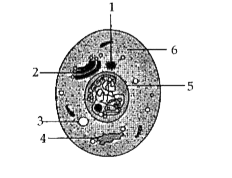
Label the parts 1 - 4.
View Solution
