In the adjoining figure, p||q. Find the unknown angles.
To solve the problem of finding the unknown angles in the figure where lines p and q are parallel, we can follow these steps:
1. Identify the Given Angle: We know that one of the angles, let's call it angle f, is given as 125 degrees.
2. Find Angle f: Since angle f and the angle adjacent to it (let's call it angle t), form a linear pair, we can use the property of linear pairs. The sum of angles in a linear pair is 180 degrees.
\(
\text{Angle } t + \text{Angle } f = 180^\circ
\)
Substituting the value of angle f:
\(
t + 125^\circ = 180^\circ
\)
Rearranging gives:
\(
t = 180^\circ - 125^\circ = 55^\circ
\)
3. Find Angle e: Angle e is vertically opposite to angle f (since two lines intersect), and vertically opposite angles are equal. Therefore:
\(
\text{Angle } e = \text{Angle } f = 55^\circ
\)
4. Find Angle a: Since lines p and q are parallel and tu is a transversal, angle f and angle a are alternate interior angles. Thus:
\(
\text{Angle } a = \text{Angle } f = 55^\circ
\)
5. Find Angle c: Angle c is vertically opposite to angle a. Therefore:
\(
\text{Angle } c = \text{Angle } a = 55^\circ
\)
6. Find Angle b: Angle a and angle b form a linear pair. Therefore:
\(
\text{Angle } a + \text{Angle } b = 180^\circ
\)
Substituting the value of angle a:
\(
55^\circ + b = 180^\circ
\)
Rearranging gives:
\(
b = 180^\circ - 55^\circ = 125^\circ
\)
7. Find Angle d: Angle d is corresponding to angle b (since lines p and q are parallel and tu is a transversal). Therefore:
\(
\text{Angle } d = \text{Angle } b = 125^\circ
\)
Summary of Angles:
- Angle a=55∘
- Angle b=125∘
- Angle c=55∘
- Angle d=125∘
- Angle e=55∘
- Angle f=125∘
\(
\text{Angle } t + \text{Angle } f = 180^\circ
\)
Substituting the value of angle f:
\(
t + 125^\circ = 180^\circ
\)
Rearranging gives:
\(
t = 180^\circ - 125^\circ = 55^\circ
\)
\(
\text{Angle } e = \text{Angle } f = 55^\circ
\)
\(
\text{Angle } a = \text{Angle } f = 55^\circ
\)
\(
\text{Angle } c = \text{Angle } a = 55^\circ
\)
\(
\text{Angle } a + \text{Angle } b = 180^\circ
\)
Substituting the value of angle a:
\(
55^\circ + b = 180^\circ
\)
Rearranging gives:
\(
b = 180^\circ - 55^\circ = 125^\circ
\)
\(
\text{Angle } d = \text{Angle } b = 125^\circ
\)
- Angle a=55∘
- Angle b=125∘
- Angle c=55∘
- Angle d=125∘
- Angle e=55∘
- Angle f=125∘
Topper's Solved these Questions
Similar Questions
In each of the following figures AB∣∣CD. Find the unknown angles, giving reasons

View SolutionIn each of the following figures AB∣∣CD. Find the unknown angles, giving reasons

View SolutionIn the adjoining figure find ∠x
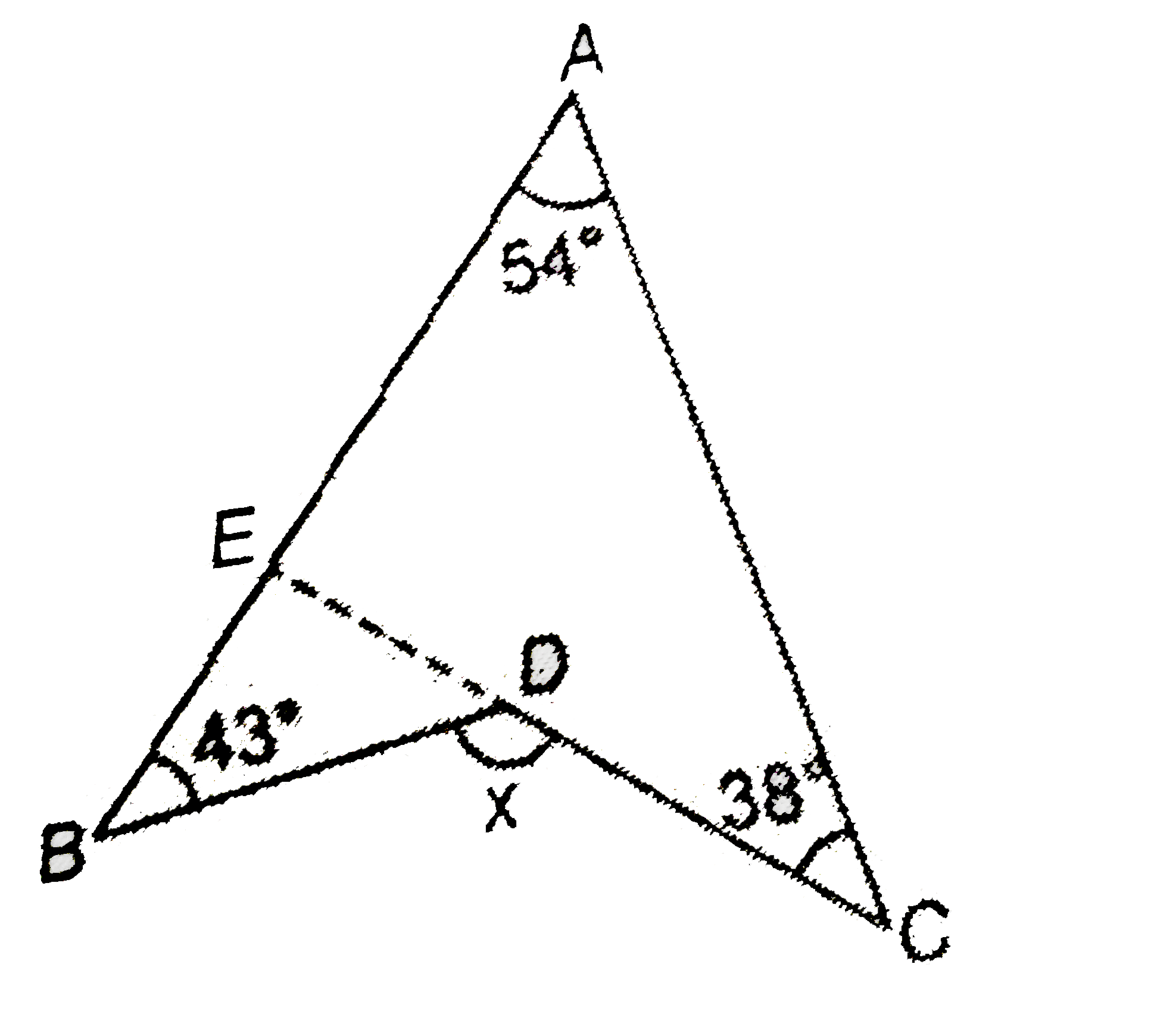
View SolutionIn the adjoining figure find ∠x
View SolutionIn the adjoining figure AB||CD, find x and y

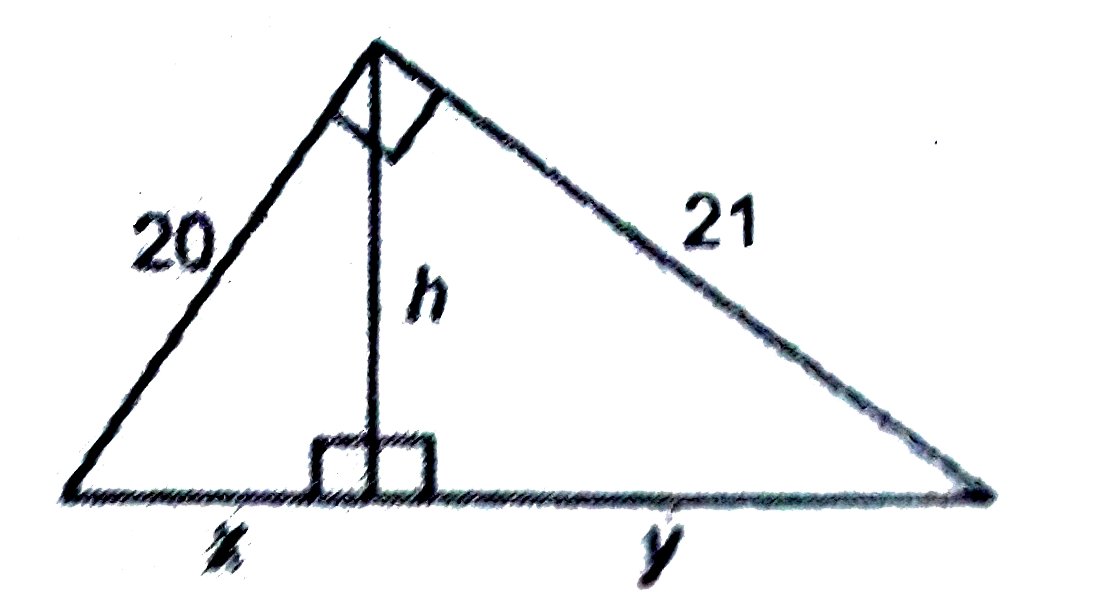
View SolutionIn the adjoining figure, find x,y and h.
View Solution(i) In the adjoining figure, find the value of ∠CBE.

(ii) In the adjoining figure, two lines PAB and PDC cut a circle at points A,B,C and D. if ∠PAD=60∘,then find the value of ∠BCD.
View SolutionIn the adjoining figure, find the value of tan B.

View SolutionIn the adjoining figure , find tan P -cot R.

View SolutionIn the adjoining figure, find the measure of angle FEB, if the lengths of sides AD, DF and FE are equal and ∠ACB=65∘.

View Solution
