From a circular card sheet of radius 14cm, two circles of radius 3.5cm and a rectangle of length 3cm and breadth 1cm are removed. (as shown in the adjoining figure). Find the area of the remaining sheet. (Take π=227)
To find the area of the remaining sheet after removing two circles and a rectangle from a circular card sheet, we can follow these steps:
Step 1: Calculate the area of the circular card sheet.
The formula for the area of a circle is:
Area=πr2
Given that the radius r=14 cm and π=227:
Area of circular card sheet=227×(14)2
Calculating (14)2:
(14)2=196
Now substituting back:
Area=227×196=22×1967
Calculating 1967=28:
Area=22×28=616 cm2
Step 2: Calculate the area of one smaller circle.
The radius of the smaller circles is 3.5 cm. Using the same formula:
Area of one smaller circle=πr2=227×(3.5)2
Calculating (3.5)2:
(3.5)2=12.25
Now substituting back:
Area=227×12.25
To simplify 12.25:
12.25=1225100=494
So,
Area=227×494=22×4928=107828=38.5 cm2
Step 3: Calculate the area of two smaller circles.
Since there are two smaller circles:
Area of two smaller circles=2×38.5=77 cm2
Step 4: Calculate the area of the rectangle.
The area of a rectangle is given by:
Area=length×breadth
Given length = 3 cm and breadth = 1 cm:
Area of rectangle=3×1=3 cm2
Step 5: Calculate the area of the remaining sheet.
Now, we subtract the areas of the two circles and the rectangle from the area of the circular card sheet:
Area of remaining sheet=Area of circular card sheet−Area of two smaller circles−Area of rectangle
Substituting the values:
Area of remaining sheet=616−77−3
Calculating:
Area of remaining sheet=616−80=536 cm2
Final Answer:
The area of the remaining sheet is 536 cm2.
---
The formula for the area of a circle is:
Area=πr2
Given that the radius r=14 cm and π=227:
Area of circular card sheet=227×(14)2
Calculating (14)2:
(14)2=196
Now substituting back:
Area=227×196=22×1967
Calculating 1967=28:
Area=22×28=616 cm2
The radius of the smaller circles is 3.5 cm. Using the same formula:
Area of one smaller circle=πr2=227×(3.5)2
Calculating (3.5)2:
(3.5)2=12.25
Now substituting back:
Area=227×12.25
To simplify 12.25:
12.25=1225100=494
So,
Area=227×494=22×4928=107828=38.5 cm2
Since there are two smaller circles:
Area of two smaller circles=2×38.5=77 cm2
The area of a rectangle is given by:
Area=length×breadth
Given length = 3 cm and breadth = 1 cm:
Area of rectangle=3×1=3 cm2
Now, we subtract the areas of the two circles and the rectangle from the area of the circular card sheet:
Area of remaining sheet=Area of circular card sheet−Area of two smaller circles−Area of rectangle
Substituting the values:
Area of remaining sheet=616−77−3
Calculating:
Area of remaining sheet=616−80=536 cm2
The area of the remaining sheet is 536 cm2.
Topper's Solved these Questions
- PERIMETER AND AREABOOK - NCERT ENGLISHCHAPTER - PERIMETER AND AREAEXERCISE - EXERCISE 11.2
8 Videos
- PERIMETER AND AREABOOK - NCERT ENGLISHCHAPTER - PERIMETER AND AREAEXERCISE - EXERCISE 11.4
8 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE 5.2
6 Videos
- RATIONAL NUMBERSBOOK - NCERT ENGLISHCHAPTER - RATIONAL NUMBERSEXERCISE - EXERCISE 9.2
4 Videos
Similar Questions
Knowledge Check
Find the area of a rectangle of length 3.2cm and breadth 2.8cm.
A8.96 sq. cmB8.06 sq. cmC8 sq. cmD7.66 sq. cmFind the ara of a rectangle of length 12 cm and breadth 8.5cm.
A109 sq. cmB102 sq. cmC106 sq. cmD108 sq. cmFind the Area of a rectangle whose length is 25 cm and breadth is 18 cm.
A550cm2B450cm2C550cm2D750cm2
Find the area of rectangle whose length is 5.7cm and breadth is 3 cm.
View SolutionWhat is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the adjoining figure. Find the area of the shaded region.
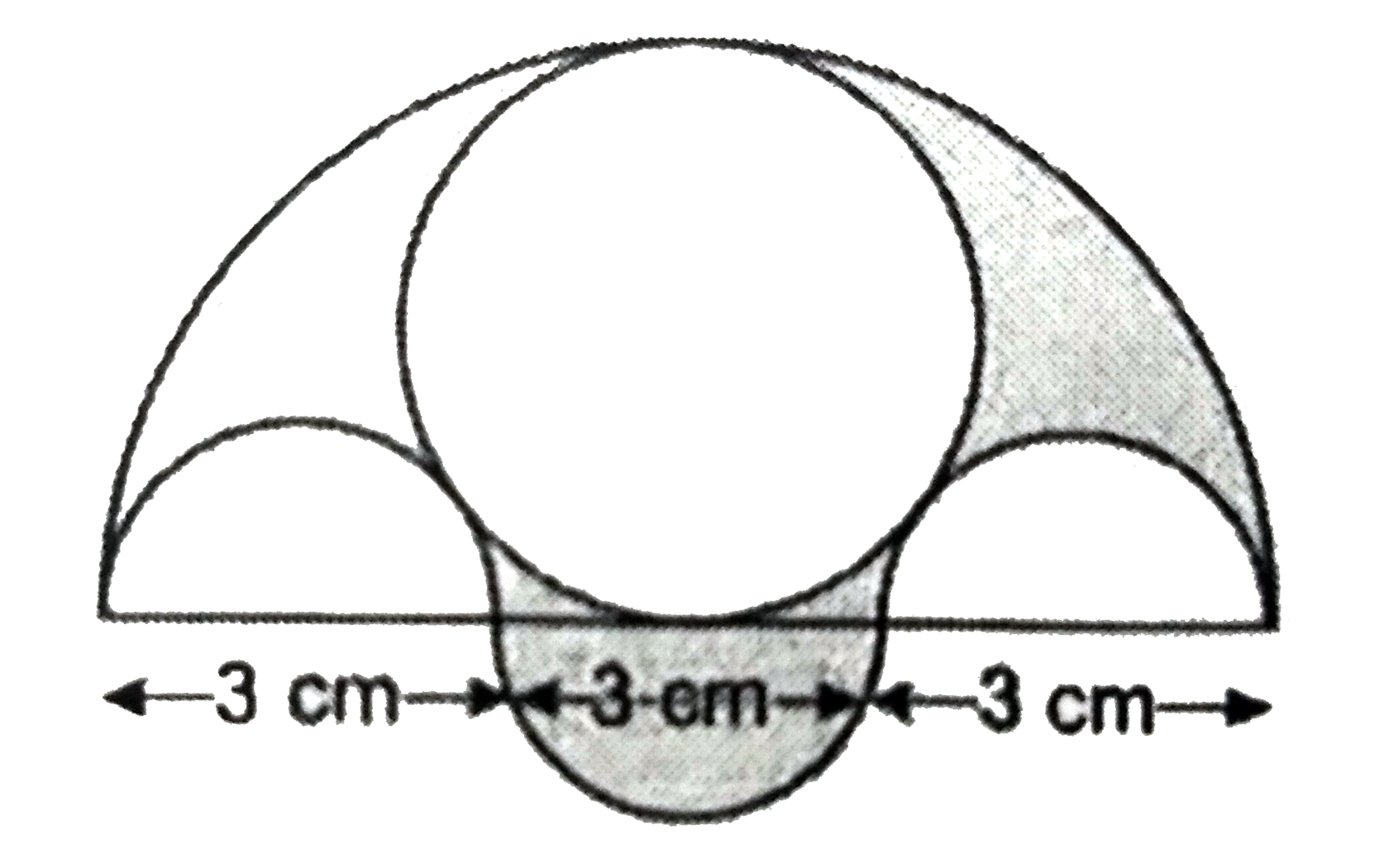
View SolutionFind the area of a rectangle whose length is 5.7 cm and breadth is 3.5 cm.
View SolutionA girl formed of design in a circle of radius 42 cm leaving an equilateral triangle ABC in the middle as shown in the figure. Find the corvered area of the design. (Use √3=1.73andπ=227)

View Solution
