The adjoining figure represents a rectangular lawn with a circular flower bed in the middle. Find:
(i) the area of the whole land
(ii) the area of the flower bed
(iii) the area of the lawn excluding the area of the flower bed
(iv) the circumference of the flower bed.
To solve the problem step by step, we will find the required areas and circumference based on the information provided.
Step 1: Find the Area of the Whole Land (Rectangular Lawn)
The area of a rectangle is calculated using the formula:
Area=Length×Breadth
Given:
- Length = 10 meters
- Breadth = 5 meters
Calculating the area:
Area of the whole land=10m×5m=50m2
Step 2: Find the Area of the Flower Bed (Circular)
The area of a circle is calculated using the formula:
Area=πr2
Given:
- Radius r=2 meters
- Using π≈3.14
Calculating the area:
Area of the flower bed=3.14×(2m)2=3.14×4=12.56m2
Step 3: Find the Area of the Lawn Excluding the Area of the Flower Bed
To find the area of the lawn excluding the flower bed, we subtract the area of the flower bed from the area of the whole land:
Area of the lawn excluding flower bed=Area of whole land−Area of flower bed
Calculating the area:
Area=50m2−12.56m2=37.44m2
Step 4: Find the Circumference of the Flower Bed
The circumference of a circle is calculated using the formula:
Circumference=2πr
Given:
- Radius r=2 meters
- Using π≈3.14
Calculating the circumference:
Circumference of the flower bed=2×3.14×2m=4×3.14=12.56m
Summary of Answers:
(i) Area of the whole land: 50m2
(ii) Area of the flower bed: 12.56m2
(iii) Area of the lawn excluding the flower bed: 37.44m2
(iv) Circumference of the flower bed: 12.56m
The area of a rectangle is calculated using the formula:
Area=Length×Breadth
- Length = 10 meters
- Breadth = 5 meters
Area of the whole land=10m×5m=50m2
The area of a circle is calculated using the formula:
Area=πr2
- Radius r=2 meters
- Using π≈3.14
Area of the flower bed=3.14×(2m)2=3.14×4=12.56m2
To find the area of the lawn excluding the flower bed, we subtract the area of the flower bed from the area of the whole land:
Area of the lawn excluding flower bed=Area of whole land−Area of flower bed
Area=50m2−12.56m2=37.44m2
The circumference of a circle is calculated using the formula:
Circumference=2πr
- Radius r=2 meters
- Using π≈3.14
Circumference of the flower bed=2×3.14×2m=4×3.14=12.56m
(i) Area of the whole land: 50m2
(ii) Area of the flower bed: 12.56m2
(iii) Area of the lawn excluding the flower bed: 37.44m2
(iv) Circumference of the flower bed: 12.56m
Topper's Solved these Questions
- PERIMETER AND AREABOOK - NCERT ENGLISHCHAPTER - PERIMETER AND AREAEXERCISE - EXERCISE 11.3
17 Videos
- PERIMETER AND AREABOOK - NCERT ENGLISHCHAPTER - PERIMETER AND AREAEXERCISE - EXERCISE 11.2
8 Videos
- PERIMETER AND AREABOOK - NCERT ENGLISHCHAPTER - PERIMETER AND AREAEXERCISE - EXERCISE 11.1
8 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE 5.2
6 Videos
- RATIONAL NUMBERSBOOK - NCERT ENGLISHCHAPTER - RATIONAL NUMBERSEXERCISE - EXERCISE 9.2
4 Videos
Similar Questions
Find the area of the flower bed (with semi-circular ends) shown in figure.

View SolutionA circular flower bed is surrounded by a path 4m wide. The diameter of the flower bed is 66m. What is the area of this path ? (π=3.14)
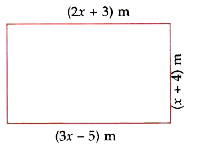
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
View SolutionEach side of a square flower bed is 2 m 80 cm long. It is extended by digging a strip 30 cm wide all around it. Find the area of the enlarged flower bed and also the increase in the area of the flower bed.
View SolutionIn Fig. 19, the radius of quarter circular plot taken is 2 m and radius of the flower bed is 2 m. Find the area of the remaining field.
View SolutionThere are two circular flower beds on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
View SolutionA circular flower bed takes up half the area of a square lawn. If an edge of the lawn is 200 feet long, what is the radius of the flower bed? (Express the answer in terms of π.)
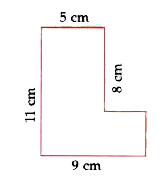
View SolutionIn the adjoining figure, all the adjacent sides are at right angles. Find:
(i) the perimeter of the figure.
(ii) the area of the figure.
View SolutionA rectangular lawn is 30 m by 20 m. It has two roads each 2 m wide running in the middle of it one parallel to the length and the other parallel to the breadth. Find the area of the roads.
View SolutionThe shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn there are flower-beds having a uniform width of 2 m.
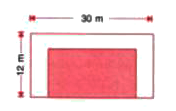
Hence, or otherwise, find the area of the flower- beds.
View Solution
