Calculate the (a) momentum and (b) de-Broglie wavelength of the electrons accelerated through a potential difference of 56V. Given, h=6.63×10−34Js,me=9.1×10−31kg,e=1.6×10−19C.
To solve the question, we need to calculate two things: (a) the momentum of the electron and (b) the de-Broglie wavelength of the electron accelerated through a potential difference of 56V.
1. Understand the relationship between kinetic energy and potential energy:
When an electron is accelerated through a potential difference V, the kinetic energy gained by the electron is equal to the work done on it by the electric field. This can be expressed as:
KE=eV
where e is the charge of the electron and V is the potential difference.
2. Express kinetic energy in terms of momentum:
The kinetic energy can also be expressed in terms of momentum p:
KE=p22m
where m is the mass of the electron.
3. Set the two expressions for kinetic energy equal to each other:
eV=p22m
4. Rearrange to find momentum p:
p2=2meV
p=√2meV
5. Substitute the known values:
- e=1.6×10−19C
- V=56V
- m=9.1×10−31kg
Plugging in these values:
p=√2×(9.1×10−31)×(1.6×10−19)×56
6. Calculate the momentum:
p=√2×9.1×10−31×1.6×10−19×56
p≈√1.6192×10−48≈4.02×10−24kg m/s
(b) Calculate the de-Broglie wavelength of the electron:
1. Use the de-Broglie wavelength formula:
The de-Broglie wavelength λ is given by:
λ=hp
where h is Planck's constant.
2. Substitute the known values:
- h=6.63×10−34Js
- p=4.02×10−24kg m/s
Plugging in these values:
λ=6.63×10−344.02×10−24
3. Calculate the de-Broglie wavelength:
λ≈1.65×10−10mor1.65Å
Final Answers:
- (a) Momentum p≈4.02×10−24kg m/s
- (b) de-Broglie wavelength λ≈1.65×10−10m or 1.65Å
When an electron is accelerated through a potential difference V, the kinetic energy gained by the electron is equal to the work done on it by the electric field. This can be expressed as:
KE=eV
where e is the charge of the electron and V is the potential difference.
The kinetic energy can also be expressed in terms of momentum p:
KE=p22m
where m is the mass of the electron.
eV=p22m
p2=2meV
p=√2meV
- e=1.6×10−19C
- V=56V
- m=9.1×10−31kg
p=√2×(9.1×10−31)×(1.6×10−19)×56
p=√2×9.1×10−31×1.6×10−19×56
p≈√1.6192×10−48≈4.02×10−24kg m/s
The de-Broglie wavelength λ is given by:
λ=hp
where h is Planck's constant.
- h=6.63×10−34Js
- p=4.02×10−24kg m/s
λ=6.63×10−344.02×10−24
λ≈1.65×10−10mor1.65Å
- (a) Momentum p≈4.02×10−24kg m/s
- (b) de-Broglie wavelength λ≈1.65×10−10m or 1.65Å
Topper's Solved these Questions
Similar Questions
What is the (a) momentum (b) speed and (c) de-Broglie wavelength of an electron with kinetic energy of 120 eV. Given h=6.6×10−34Js,me=9×10−31kg,1eV=1.6×10−19J.
View SolutionAn electron is accelerated through a potential difference of 10,000V. Its de Broglie wavelength is, (nearly): (me=9×10−31kg)
View Solution
Knowledge Check
The de Broglie wavelength of an electron with kinetic energy 120 e V is (Given h=6.63×10−34Js,me=9×10−31kg,1eV=1.6×10−19J)
A2.13Ã…B1.13Ã…C4.15Ã…D3.14Ã…When light of wavelength 400nm is incident on the cathode of photocell, the stopping potential recorded is 6V. If the wavelength of the incident light is to 600nm, calculate the new stopping potential. [Given h=6.6×10−34Js,c=3×108m/s,e=1.6×10−19C]
A1.03VB2.42VC4.97VD3.58V
If de Broglie wavelength of an electron is 0.5467 Å,
find the kinetic energy of electron in eV. Given h=6.6×10−34 Js ,
e=1.6×10−19 C, me=9.11×10−31 kg.
View SolutionDe - Broglie wavelength of an electron accelerated by a voltage of 50 V is close to
(|e|=1.6×10−19C,me=9.1×10−31)
View SolutionFind de-Broglie wavelength of electron with KE=9.6×10−19J.
View SolutionIf an electron has an energy such that its de Broglie wavelength is 5500Å, then the energy value of that electron is (h=6.6×10−34) Js, mc=9.1×10−31 kg
View SolutionWith what velocity must an electron travel so that its momentum is equal to that of a photon with a wavelength of 5000Å(h=6.6×10−34Js,me=9.1×10−31 Kg)
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructiely
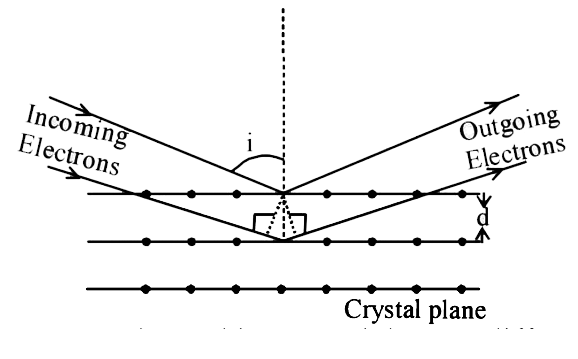
Electron accelerated by potential V are diffracted from a crystal if d=1Åandi=30∘,V should be about (h=6.6×10−34Js,me=9.1×10−31kg,e=1.6×10−19C)
View Solution
