The rate of a reaction quadruples when the temperature changes from to . Calculate the energy of activation of the reaction assuming that it does not change with temperature.
To calculate the energy of activation (Ea) for the reaction given that the rate quadruples when the temperature changes from 293 K to 313 K, we can use the Arrhenius equation. Here’s how to solve it step by step:
Step 1: Understand the relationship between rate constants and temperature
The rate of a reaction is related to the rate constant (k) by the equation:
k=Ae−EaRT
where:
- k = rate constant
- A = pre-exponential factor (frequency factor)
- Ea = activation energy
- R = universal gas constant (8.314 J/(K·mol))
- T = temperature in Kelvin
Step 2: Set up the equation for two different temperatures
For two different temperatures T1 and T2, the ratio of the rate constants can be expressed as:
k2k1=e−EaRT2/e−EaRT1
This can be rewritten using logarithms:
log(k2k1)=Ea2.303R(1T1−1T2)
Step 3: Substitute the known values
Given that the rate quadruples, we have:
- k2=4k1
Thus:
k2k1=4
Taking logarithm:
log(4)=Ea2.303R(1T1−1T2)
Substituting the values:
- T1=293K
- T2=313K
- R=8.314J/(K⋅mol)
Step 4: Calculate log(4)
We know:
log(4)=2log(2)≈2×0.301=0.602
Step 5: Calculate the temperature difference
Calculate:
1T1−1T2=1293−1313
Calculating each term:
1293≈0.003414K−1
1313≈0.003194K−1
Thus:
1293−1313≈0.003414−0.003194=0.000220K−1
Step 6: Substitute into the equation
Now substituting everything into the logarithmic equation:
0.602=Ea2.303×8.314×0.000220
Step 7: Solve for Ea
Rearranging gives:
Ea=0.602×2.303×8.314×10.000220
Calculating:
1. 0.602×2.303≈1.386
2. 1.386×8.314≈11.52
3. Ea≈11.52×10.000220≈52400J/mol
Step 8: Convert to kJ/mol
Finally, convert Joules to kilojoules:
Ea≈52.4kJ/mol
Final Answer
The energy of activation Ea is approximately 52.4 kJ/mol.
The rate of a reaction is related to the rate constant (k) by the equation:
k=Ae−EaRT
where:
- k = rate constant
- A = pre-exponential factor (frequency factor)
- Ea = activation energy
- R = universal gas constant (8.314 J/(K·mol))
- T = temperature in Kelvin
For two different temperatures T1 and T2, the ratio of the rate constants can be expressed as:
k2k1=e−EaRT2/e−EaRT1
This can be rewritten using logarithms:
log(k2k1)=Ea2.303R(1T1−1T2)
Given that the rate quadruples, we have:
- k2=4k1
Thus:
k2k1=4
Taking logarithm:
log(4)=Ea2.303R(1T1−1T2)
- T1=293K
- T2=313K
- R=8.314J/(K⋅mol)
We know:
log(4)=2log(2)≈2×0.301=0.602
Calculate:
1T1−1T2=1293−1313
Calculating each term:
1293≈0.003414K−1
1313≈0.003194K−1
Thus:
1293−1313≈0.003414−0.003194=0.000220K−1
Now substituting everything into the logarithmic equation:
0.602=Ea2.303×8.314×0.000220
Rearranging gives:
Ea=0.602×2.303×8.314×10.000220
1. 0.602×2.303≈1.386
2. 1.386×8.314≈11.52
3. Ea≈11.52×10.000220≈52400J/mol
Finally, convert Joules to kilojoules:
Ea≈52.4kJ/mol
The energy of activation Ea is approximately 52.4 kJ/mol.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - NCERT ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercise
1 Videos
- CHEMICAL KINETICSBOOK - NCERT ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - SOLVED EXAMPLE
1 Videos
- BIOMOLECULESBOOK - NCERT ENGLISHCHAPTER - BIOMOLECULESEXERCISE - Exercise
33 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - NCERT ENGLISHCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - Exercise
32 Videos
Similar Questions
The rate of a reaction increases four times when the temperature changes from 300 K to 320 K. Calculate the energy of activation of the reaction, assuming that it does not change with temperature. (R = 8.314 JK−1mol−1)
View SolutionThe rate of a reaction increases four times when the temperature changes from 300 K to 320 K. Calculate the energy of activation of the reaction, assuming that it does not change with temperature. (R = 8.314 JK−1mol−1)
View SolutionThe rate of a reaction increases four times when the temperature changes from 300 K to 320 K. Calculate the energy of activation of the reaction, assuming that it does not change with temperature. (R = 8.314 JK−1mol−1)
View Solution(a) Explain the following terms :
(i) Order of a reaction
(ii) Molecularity of a reaction
(b) The rate of a reaction increases four times when the temperature changes from 300 K to 320 K. Calculate the energy of activation of the reaction, assuming that it does not change with temperature. (R=8.314JK−1mol−1)
View SolutionThe rate of a reaction triples when temperature changes from 20∘C to 50∘C. Calculate the energy of activation.
View SolutionThe rates of most reaction double when their temperature is raised from 298K to 308K. Calculate their activation energy.
View SolutionThe rate of reaction triples when temperature changes form 20∘C to 50∘C. Calculate the energy of activation for the reaction (R=8.314JK−1mol−1).
View SolutionThe rate of a reaction quadruples when the temperature changes from 300 to 310 K. The activation energy of this reaction is :
( Assume Activation energy and pre-exponential factor are independent of temperature, ln(2)=0.693,R=8.314J−mol−1K−1)
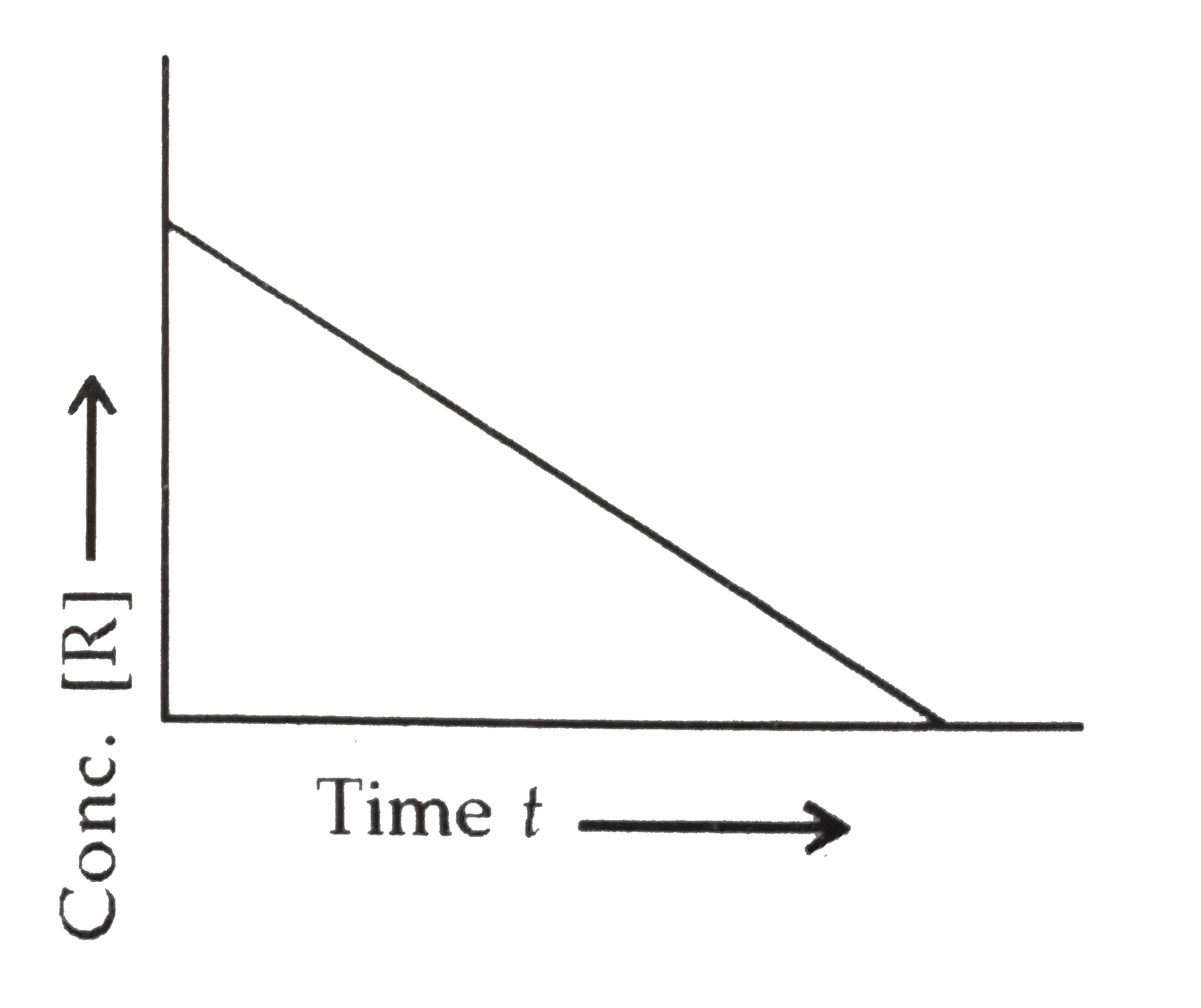
View SolutionConsider the reaction R→P for which the change in concentration of R with time is shown by the following graph:
( i) Predict the order of reaction .
( iii) What does the slope of the curve indicate ?
( b) The rate of reaction quadruples when temperature chages from 293 K of 313 K .Calculate Ea assuming that it does not chage with time [R=8.314JK−1mol−1]
View SolutionThe rate of a reaction triples when temperature changes from 50∘ C to 100∘C. Calculate the energy of activation for such a reaction. (R=8.314JK−1mol−1log3=0.4771)
View Solution
