Given below are observations on molar specific heats at room temperature of some common gases
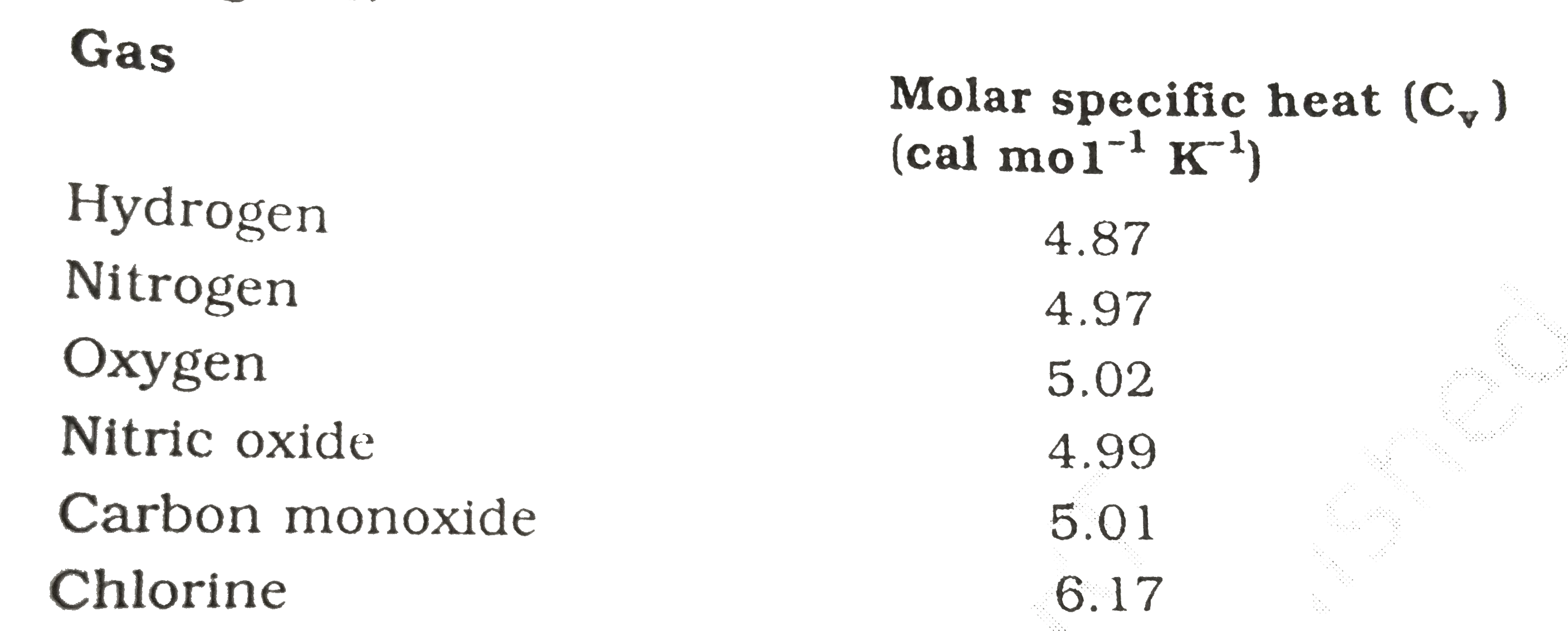
The measured molar specific heats of these gases are markedly different from those for monatomic gases. Typically, molar specific heat of a monatomic gas is 2.92 cal/mol K. Explain this difference. What can you infer from the somewhat larger (than the rest) value for chlorine ?
The gases listed in the given table are diatomic. Besides the translational degree of freedom, they have other degrees of freedom (modes of motion).
Heat must be supplied to increase the temperature of these gases. This increases the average energy of all the modes of motion. Hence, the molar specific heat of diatomic gases is more than that of monatomic gases.
If only rotational mode of motion is considered, then the molar specific
heat of a diatomic gas=52R
=52×1.98=4.95cal mol1K−1
With the exception of chlorine, all the observations in the given table
agree with(52R).This is because at room temperature, chlorine also has vibrational modes of motion besides rotational and translational modes of motion.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:NCERT ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:EXERCISE
Explore 22 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:NCERT ENGLISHChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:EXERCISE
Explore 33 Videos
- THERMODYNAMICSBook:NCERT ENGLISHChapter:THERMODYNAMICSExercise:EXERCISE
Explore 10 Videos
Similar Questions
The molar specific heat capacity of all monatomic gases is the same. Is this ture of false ? (Assumed ideal nature.)
View SolutionWhat are the two specific heat capacities of a gas and why are they different? Find the difference between the two molar heat capacities in terms of the constant R.
View SolutionA process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by W and increase in internal energy as ΔU then
W∝ΔU
or W=K1ΔU ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
PVη=K2 (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat 'C' for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat 'C' with η for a monatomic gas is plotted as in the graph shown.

For a monoatomic gas, the values of polytropic constant η for which value specific heat is negative.
View SolutionA process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by W and increase in internal energy as ΔU then
W∝ΔU
or W=K1ΔU ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
PVη=K2 (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat 'C' for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat 'C' with η for a monatomic gas is plotted as in the graph shown.

In the graph shown, the y− coordinate of point A is ( for monatomic gas )
View SolutionAn ideal gas may expands from V0 to 2V0 according to following three processes. Molar specific heat for processes b will be

View SolutionThe molar specific heat of a gas as given from the kinetic theory is 52R. If it is not specified whether it is CporCυ one could conclude that the molecules of the gas
View SolutionAn ideal monatomic gas undergoes a process where its pressure is inversely proportional to its temperature.
(a) Calculate the molar specific heat of the process.
(b) Find the work done by two moles of gas if the temperature change from T1 to T2.
View SolutionStatement - 1: An ideal gas has infinitely many molar specific heats.
Statement-2: Specific heat is amount of heat needed to raise the temperature of 1 mole of gas by 1K.
View SolutionThe molar specific heats of an ideal gas at constant volume and constant pressure are respectively 4.98 and 6.96 cal mol−1K−1. If the molecular weight of the gas be 32, then calculate the root means square speed of the molecule of the gas at 120∘C. (1 cal = 4.2 J)
View SolutionOne mole of a perfect gas expands adiabatically .As a result of this,its pressure ,temperature and volume changes from P1,T1,V1, to P2,T2,V2 respectively .If molar specific heat at volume is Cv then work done by the gas wil be ?
View Solution
