Uranium has two isotopes of masses 235 and 238 units. If both are present in uranium hexa fluoride gas, which would have the larger average speed ? If atomic mass of fluorine is 19 units, estimate the percentage difference in speed at any temperature.
To solve the problem, we need to determine which isotope of uranium (U-235 or U-238) has a larger average speed when they are both present in uranium hexafluoride (UF6) gas. We will also estimate the percentage difference in speed at any temperature.
1. Identify the Molar Mass of UF6 for Both Isotopes:
- For U-235:
Molar mass of UF6=235+6×19=235+114=349 units
- For U-238:
Molar mass of UF6=238+6×19=238+114=352 units
2. Use the Formula for Average Speed:
The average speed (v) of gas molecules is given by the equation:
v=√3kTm
where k is Boltzmann's constant, T is the temperature, and m is the mass of the gas molecule.
3. Calculate the Ratio of Speeds:
The ratio of the speeds of the two isotopes can be expressed as:
v1v2=√m2m1
where m1 is the molar mass of U-235 (349 units) and m2 is the molar mass of U-238 (352 units).
vU−235vU−238=√352349
4. Calculate the Square Root:
vU−235vU−238≈√1.0086≈1.0043
5. Determine the Percentage Difference in Speed:
The percentage difference in speed can be calculated as:
Percentage Difference=(vU−235−vU−238vU−238)×100
Using the ratio:
Percentage Difference=(1.0043−11)×100≈0.43%
Final Result:
The isotope U-235 has a larger average speed than U-238, and the percentage difference in speed at any temperature is approximately 0.43%.
- For U-235:
Molar mass of UF6=235+6×19=235+114=349 units
- For U-238:
Molar mass of UF6=238+6×19=238+114=352 units
The average speed (v) of gas molecules is given by the equation:
v=√3kTm
where k is Boltzmann's constant, T is the temperature, and m is the mass of the gas molecule.
The ratio of the speeds of the two isotopes can be expressed as:
v1v2=√m2m1
where m1 is the molar mass of U-235 (349 units) and m2 is the molar mass of U-238 (352 units).
vU−235vU−238=√352349
vU−235vU−238≈√1.0086≈1.0043
The percentage difference in speed can be calculated as:
Percentage Difference=(vU−235−vU−238vU−238)×100
Using the ratio:
Percentage Difference=(1.0043−11)×100≈0.43%
The isotope U-235 has a larger average speed than U-238, and the percentage difference in speed at any temperature is approximately 0.43%.
Topper's Solved these Questions
Similar Questions
Oxidation number is the charge which an atom of an element has in its ion or appears to have when present in the combined state. It is also called oxidation state. Oxidation number of any atom in the elementary state is zero. Oxidation number of a monoatomic ion is equal to the charge on it. In compounds of metals with non metals, metals have positive oxidation number while non metals have negative oxidation numbers. In compounds of two difference elements, the more electronegative element has negative oxidation number whereas the other has positive oxidation number. In complex ions, the sum of the oxidation number of all the atoms is equal to the charge on the ion. If a compound contains two or more atoms of the same element, they may have same or different oxidation states according as their chemical bonding is same or different.
A compound of Xe and F is found to have 53.3% Xe (atomic weight =133). Oxidation number of Xe in this compound is
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
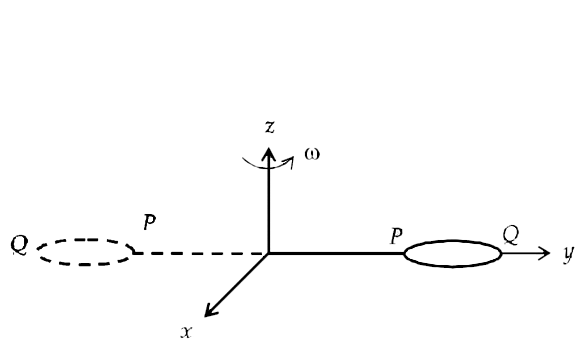
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
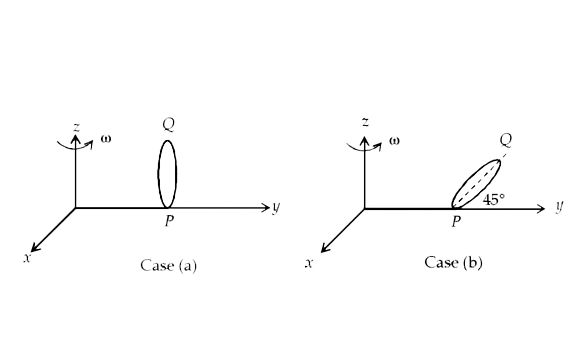
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion …. of its centre of mass about an axis, and (ii) its motion about an instantaneous axis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless stick, as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω , the motion at any instant can be taken as a combination of (i) a rotation of the centre of mass of the disc about the z-axis, and (ii) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case.

Now consider two similar systems as shown in the figure: case (a) the disc with its face vertical and parallel to x-z plane, case (b) the disc with its face making an angle of 45° with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the system are rotated with constant angular speed ω about the z-axis
Which of the following statement regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct ?
View SolutionA smooth vertical tube having two different cross sections is open from both the ends but closed by two sliding pistions as shown in Fig. and tied with an inextensible string. One mole of an ideal gas is enclosed between the piston The difference in cross-sectional areas of the two pistons is given ΔS. The masses of piston are m1 and m2 for larger and smaller one, respectively. Find the temperature by which tube is raised so that the pistons will be displaced by a distance l. Take atmospheric pressure equal to P0

View SolutionA smooth vertical tube having two different cross sections is open from both the ends but closed by two sliding pistions as shown in Fig. and tied with an inextensible string. One mole of an ideal gas is enclosed between the piston The difference in cross-sectional areas of the two pistons is given ΔS. The masses of piston are m1 and m2 for larger and smaller one, respectively. Find the temperature by which tube is raised so that the pistons will be displaced by a distance l. Take atmospheric pressure equal to P0

View SolutionA tightly-wound, long solenoid has n turns per unit length, a radius r and carries a current i. A particle having charge q and mass m is projected from a point on the axis in a direction perpendicular to the axis. What can be the maximum speed for which the particle does not strike the solenoid?
View SolutionA tightly-wound, long solenoid has n turns per unit length, a radius r and carries a current i. A particle having charge q and mass m is projected from a point on the axis in a direction perpendicular to the axis. What can be the maximum speed for which the particle does not strike the solenoid?
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
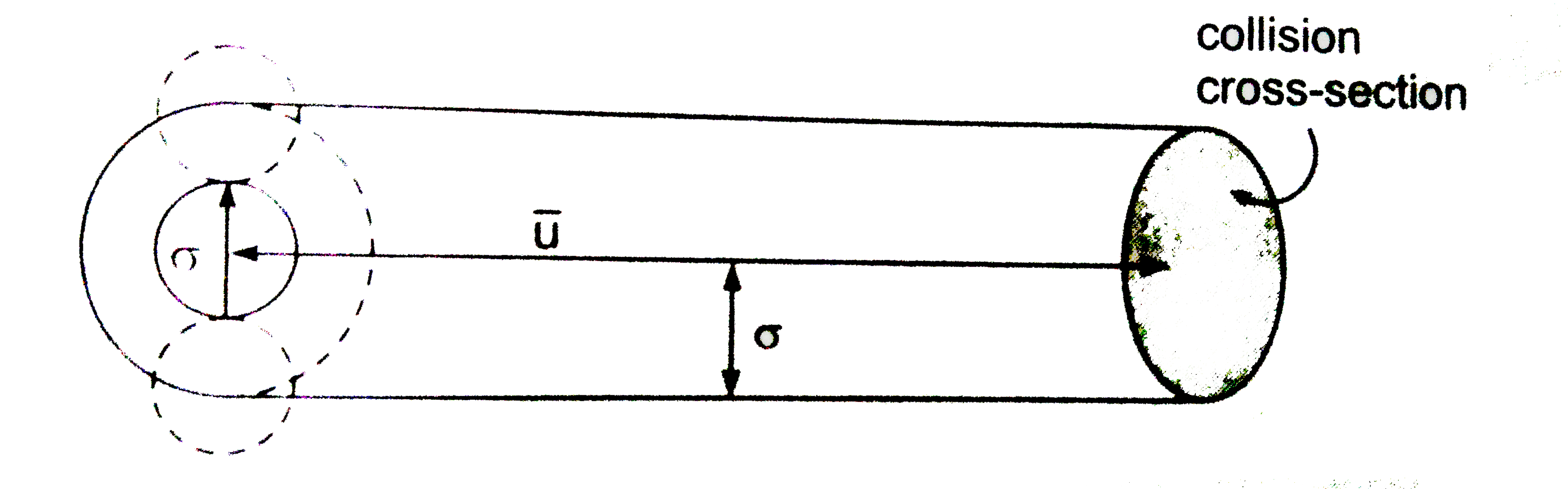
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate ratio of collision frequencies (Z11)(A:B:C) of following for the three gases.
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
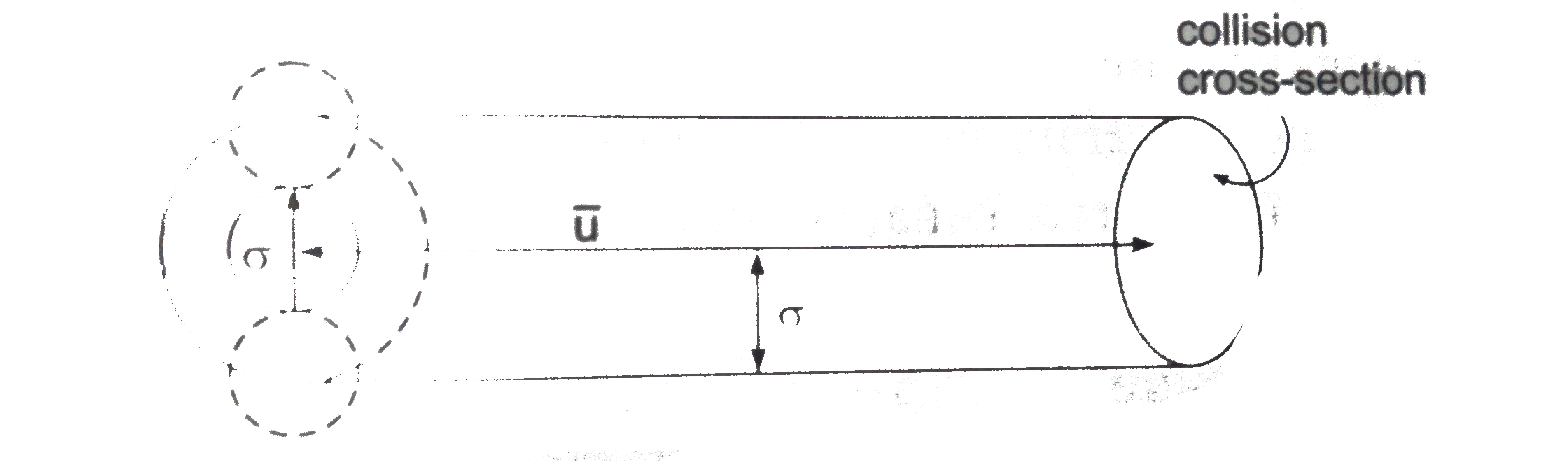
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A current of 1 A flows through a copper wire. The number of electrons passing through any cross-section of the wire in 1.6 sec is (charge of a electron = 1.6 xx 10^(-19 c).
View Solution
