The terminology of different parts of the electromagnetic spectrum is given in the text. Use the formula E = h ν (for energy of a quantum of radiation: photon) and obtain the photon energy in units of eV for different parts of the electromagnetic spectrum. In what way are the different scales of photon energies that you obtain related to the sources of electromagnetic radiation?
To solve the problem of calculating the photon energy in units of electron volts (eV) for different parts of the electromagnetic spectrum using the formula E=hν, we can follow these steps:
Step 1: Understand the Formula
The energy of a photon is given by the equation:
E=hν
where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34Js),
- ν is the frequency of the photon.
Step 2: Relate Frequency to Wavelength
We can also express frequency in terms of wavelength (λ):
ν=cλ
where:
- c is the speed of light (3×108m/s).
Step 3: Substitute Frequency into the Energy Equation
Substituting the expression for frequency into the energy equation gives:
E=hcλ
Step 4: Convert Energy to Electron Volts
To convert the energy from joules to electron volts, we use the conversion factor:
1eV=1.6×10−19J
Thus, the energy in eV can be expressed as:
E(in eV)=hcλ×1.6×10−19
Step 5: Calculate Photon Energy for Different Wavelengths
Now, we can calculate the photon energy for various wavelengths in the electromagnetic spectrum:
1. For λ=10−3m (1 mm, microwave region):
E=(6.626×10−34)(3×108)10−3×1.6×10−19≈1.24×10−10eV
2. For λ=1m (radio waves):
E=(6.626×10−34)(3×108)1×1.6×10−19≈1.24×10−7eV
3. For λ=10−6m (infrared region):
E=(6.626×10−34)(3×108)10−6×1.6×10−19≈1.24×10−4eV
4. For λ=10−9m (ultraviolet region):
E=(6.626×10−34)(3×108)10−9×1.6×10−19≈1.24×10−1eV
Step 6: Analyze the Relationship Between Photon Energy and Sources of Electromagnetic Radiation
The different scales of photon energies correspond to the sources of electromagnetic radiation. For example:
- Radio waves (long wavelength, low energy) are produced by oscillating charges in antennas.
- Microwaves (shorter wavelength, higher energy) are used in microwave ovens and are produced by certain electronic devices.
- Infrared radiation is emitted by warm objects and is used in thermal imaging.
- Ultraviolet radiation can be produced by high-energy processes such as electric discharges or the sun.
Summary
The energy of photons varies significantly across the electromagnetic spectrum, with longer wavelengths corresponding to lower energies and shorter wavelengths corresponding to higher energies. This variation is directly related to the physical processes that produce these types of radiation.
The energy of a photon is given by the equation:
E=hν
where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34Js),
- ν is the frequency of the photon.
We can also express frequency in terms of wavelength (λ):
ν=cλ
where:
- c is the speed of light (3×108m/s).
Substituting the expression for frequency into the energy equation gives:
E=hcλ
To convert the energy from joules to electron volts, we use the conversion factor:
1eV=1.6×10−19J
Thus, the energy in eV can be expressed as:
E(in eV)=hcλ×1.6×10−19
Now, we can calculate the photon energy for various wavelengths in the electromagnetic spectrum:
E=(6.626×10−34)(3×108)10−3×1.6×10−19≈1.24×10−10eV
E=(6.626×10−34)(3×108)1×1.6×10−19≈1.24×10−7eV
E=(6.626×10−34)(3×108)10−6×1.6×10−19≈1.24×10−4eV
E=(6.626×10−34)(3×108)10−9×1.6×10−19≈1.24×10−1eV
The different scales of photon energies correspond to the sources of electromagnetic radiation. For example:
- Radio waves (long wavelength, low energy) are produced by oscillating charges in antennas.
- Microwaves (shorter wavelength, higher energy) are used in microwave ovens and are produced by certain electronic devices.
- Infrared radiation is emitted by warm objects and is used in thermal imaging.
- Ultraviolet radiation can be produced by high-energy processes such as electric discharges or the sun.
The energy of photons varies significantly across the electromagnetic spectrum, with longer wavelengths corresponding to lower energies and shorter wavelengths corresponding to higher energies. This variation is directly related to the physical processes that produce these types of radiation.
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBook:NCERT ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Exercise
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercise
Explore 17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NCERT ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise
Explore 37 Videos
Similar Questions
Knowledge Check
The photon energy in units of eV for electromagnetic waves of wavelength 2 cm is
A2.5×10−19B5.2×1016C3.2×10−16D6.2×10−5
In figure E1andE2 represent some of the energy levels of the hydrogen atom.
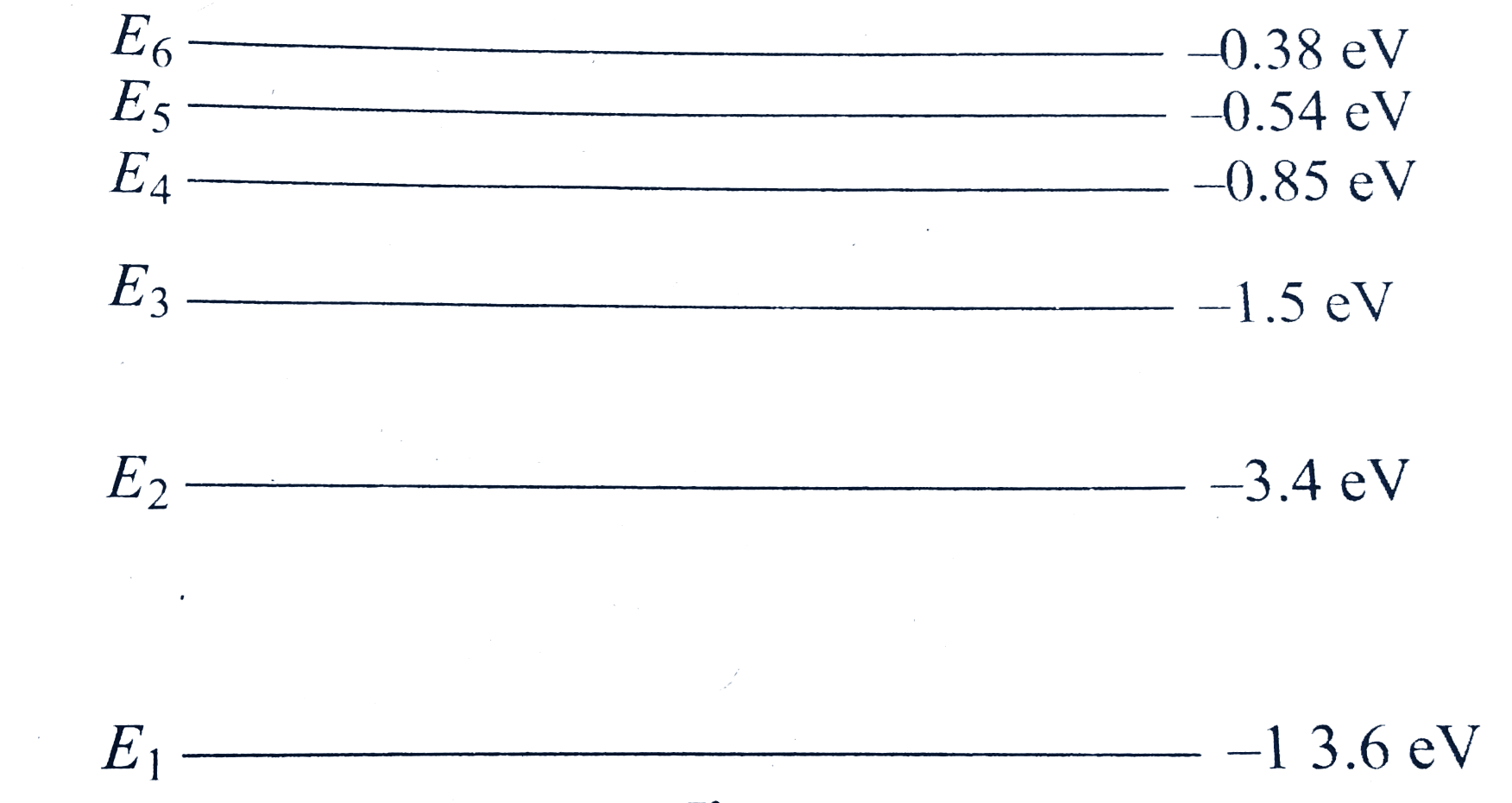
Which one of the following transitions produced a photon of wavelength in the ultraviolet region of the electromagnetic spectrum?
View Solution(a) Identify the part of electromagnetic spectrum used in (i) radar and (ii) eye surgery. Write their frequency range.
(b) Prove that average energy density of the oscillating electric field is equal to that of oscillating magnetic field.
View SolutionWhen an electron falls from a higher energy to a lower energy level, the difference in the energies appears in the forms of electromagnetic radiation. Why cannot it be emitted as other forms of energy?
View SolutionPhoton is quantum of radiation with energy E =hv where v is frequency and h is Planck's constant. The dimensions of h are the same as that of
View SolutionAn electron is accelerated through a potential difference of 64volts. What is the de-broglie wavelength associated with it? To which part of the electromagnetic spectrum does this value of wavelength correspond?
View SolutionStatement 1: In process of photoelectric emission, all emitted electrons do not have same kinetic energy.
Statement 2: If radiation falling on photosensitive surface of a metal consists of different wavelengths, then energy acquired by electrons absorbing photons of different wavelengths shall be different.
View SolutionCalculate
(a) The wavelength and the frequency of the Hβ line of the Balmer series for hydrogen.
(b) Find the longest and shortest wavelengths in the Lyman series for hydrogen. In what region of the electromagnetic spectrum does this series lie ?
(c) Whenever a photon is emitted by hydrogen in Balmer series, it is followed by another photon in LYman series. What wavelength does this latter photon correspond to ?
(d) The wavelength of the first of Lyman series for hydrogen is identical to that of the second line of Balmer series for some hydrogen-like ion X. Find Z and energy for first four levels.
View Solution
