A diagonal of parallelogram divides it into two congruent triangles.
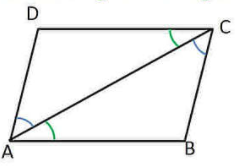
opposites sides of parallelogram are parallel. Thus
So, AB∣∣DC and AD∣∣BC.
In △ABC and △ADC,
∠BAC=∠DCA
AC=AC (common)
∠DAC=∠BCA
Thus, with ASA congruency, △ABC and △ADC are congruent.
Topper's Solved these Questions
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 8.2
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 8.3
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 7.8
1 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- NUMBER SYSTEMSBOOK - NCERT ENGLISHCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
2 Videos
Similar Questions
Prove that A diagonal of a parallelogram divides it into two triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area. GIVEN : A parallelogram ABCD . The diagonals AC and BD intersect at O. TO PROVE : ar(OAB)=ar(OBC)=ar(OCD)=ar(AOD)
View SolutionThe median of a triangle divides it into two (a)congruent triangle (b) isosceles triangles (c)right triangles (d) triangles of equal areas
View SolutionThe median of a triangle divides it into two
View SolutionThe diagonal AC of a quadrilateral ABCD divides it into two triangles of equal areas. Prove that diagonal AC bisects the diagonal BD.
View SolutionShow that the segment joining the mid-points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms.
View SolutionIf the two diagonals of a parallelogram are equal, it is a rectangle.
View SolutionIf the diagonals of a parallelogram are equal and intersect at right angles, then the parallelogram is a square.
View Solution
