Equal chords of congruent circles are equidistant from the corresponding centres.
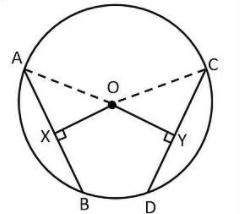
Since OX⊥AB
Perpendicular from the center to the chord, bisects the chord,
AX=BX=AB2
Similarly,
CY=DY=CD2
AB=CD (given)
Thus,
AX=CY
In △AOX and △COY,
∠OXA=∠OYC (Perpendicular angles)
OA−OC (radius)
AX=CY
By RHS rule, △AOX and △COY are congruent.
OX=OY (CPCT)
Topper's Solved these Questions
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.7
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.8
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.5
1 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- NUMBER SYSTEMSBOOK - NCERT ENGLISHCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
2 Videos
Similar Questions
Prove Chords of congruent circles which are equidistant from the corresponding centres, are equal.
View SolutionEqual chords of a circle are equidistant from the centre.
View SolutionIf the angles subtended by two chords of congruent circles at the corresponding centres are equal, then Prove chords are equal.
View Solutionequal chords are equidistant from each other
View SolutionChords of a circle which are equidistant from the centre are equal.
View SolutionIf two chord of a circle (or of congruent circles) are equal, then their corresponding arcs. (minor, major or semi-circular) are congruent.
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionProve Equal chords of congruent circles subtend equal angles at the centre.
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View Solution
