Theorem:- If the line segment joining two points subtends equal angles at two other points lying on the same side of the line segment; the four points are concyclic. i.e lie on the same circle.
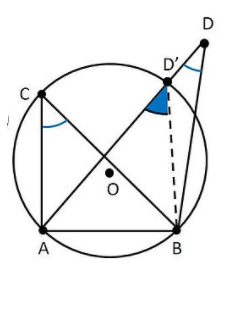
Since ,, are non-collinear, one circle passes through them. raw a circle with center .
Let not lie on circle. Let circle intersect at .
(Angle in same segment)
But,
Thus,
This may only happen if and only if and coincides. Thus, point lie on circle.
Topper's Solved these Questions
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.11
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.12
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.9
1 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- NUMBER SYSTEMSBOOK - NCERT ENGLISHCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
2 Videos
Similar Questions
A line segments has two end points.
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection
View SolutionThe mid point of the line segment joining the points (−5,7)and(−1,3) is
View SolutionProve that the line joining centres of two interesting circles subtends equal angles at the two points of intersection.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionShow that the mid-point of the line segment joining the points (5,7) and (3,9) is also the mid-point of the line segment joining the points (8,6) and (0,10) .
View SolutionProve that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
View SolutionProve that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
View SolutionProve that the line segments joining the mid-points of the sides of a triangle from four triangles, each of which is similar to the original triangle.
View Solution
