नियत बलों एवं के द्वारा कार्यशील एक कण को बिन्दु से बिन्दु तक विस्थापित किया जाता है। बलों के द्वारा किया गया कुल कार्य SI मात्रक में होता है
20
40
50
30
The correct Answer is:B
यहाँ
विस्थापन
बालो द्वारा किया गया कार्य,
Topper's Solved these Questions
- कार्य, ऊर्जा और शक्ति BOOK - NCERT FINGERTIPS HINDICHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - बहुविकल्प प्रश्न पिटारा (गतिज ऊर्जा)
15 Videos
- कार्य, ऊर्जा और शक्ति BOOK - NCERT FINGERTIPS HINDICHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - बहुविकल्प प्रश्न पिटारा (किसी परिवर्ती बल द्वारा किया गया कार्य)
4 Videos
- कार्य, ऊर्जा और शक्ति BOOK - NCERT FINGERTIPS HINDICHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- कणों के निकाय घूर्णी गतिBOOK - NCERT FINGERTIPS HINDICHAPTER - कणों के निकाय घूर्णी गतिEXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- गति के नियम BOOK - NCERT FINGERTIPS HINDICHAPTER - गति के नियम EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
Similar Questions
कॉस्मिक तरंग प्रयोग में, एक इलेक्ट्रॉन एवं एक प्रोटॉन का पता लगता है, इलेक्ट्रॉन की गतिज ऊर्जा 10 keV एवं प्रोटॉन की गतिज ऊर्जा 100 kev है। इनकी चालों का अनुपात ज्ञात कीजिए। (जहाँ me एवं mp क्रमशः इलेक्ट्रॉन एवं प्रोटॉन के द्रव्यमान हैं)
View Solutionचित्र में दिखाए गए अनुसार, x दूरी से परिवर्तन के साथ किसी वस्तु पर एक बल F कार्यरत है। x = 0 से x = 20 m तक किसी वस्तु को गति करने में बल द्वारा किया गया कार्य है
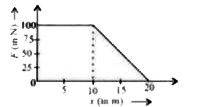
View Solutionअभिकथनः दो पिण्डों के लिए, न्यूटन के तीसरे नियम से उनके मध्य उत्पन्न पारस्परिक बलों का योग शून्य होता है।
तर्कः दो बलों के द्वारा किए गए कार्य के योग को हमेशा निरस्त करना चाहिए।
View Solutionनिम्न प्रश्न में, अभिकथन के वक्तव्य के बाद तर्क के वक्तव्य को दिया गया है। सही विकल्प पर निशान लगाइए।
अभिकथनः किसी निकाय के द्रव्यमान केन्द्र की गति का निर्धारण करने के लिए, निकाय के आंतरिक बलों का ज्ञान होना आवश्यक होता है।
तर्कः इस उद्देश्य के लिए हमें निकाय पर बाह्य बलों को जानने की आवश्यकता नहीं होती है।
View Solutionअभिकथन: किसी वस्तु की गति को बनाए रखने के लिए एक बाहरी बल की आवश्यकता होती है।
तर्क: कुल बाह्य बल शून्य है तो विरामावस्था वाली वस्तु विरामावस्था में ही रहेगी तथा गतिमान वस्तु एकसमान वेग से गतिमान रहती है।
View Solutionनिम्नलिखित सदिशों के अदिश गुणनफल ज्ञात कीजिए -
(i)4ˆi+4ˆj−ˆk और5ˆi+ˆj+2ˆk
(ii)3ˆi+4ˆj और ˆi+4ˆj−ˆk
(iii)5ˆj−10ˆk और3ˆi−8ˆj−2ˆk
(iv)ˆi−ˆj+ˆk और ˆi+ˆj−ˆk
View Solutionनिम्निलिखित सदिशों के बीच का कोण ज्ञात कीजिए -
(i) 2ˆi−ˆj+2ˆk और 3ˆi+3ˆj+4ˆk
(ii)2ˆi+ˆj+3ˆk और 3ˆi−2ˆj+ˆk
View Solution[ˆiˆkˆj]+[ˆkˆjˆi]+[ˆjˆkˆi] is equal to
View Solution(a⋅ˆi)ˆi+(a⋅ˆj)ˆj+(a⋅ˆk)ˆk is equal to
View SolutionIf a=ˆi+ˆj+ˆkandb=ˆi−ˆj, then vectors (a⋅ˆi+ˆi+(a⋅ˆj+(a⋅ˆk)ˆk,(b⋅ˆi)ˆi+(bˆj)ˆj+(b⋅ˆk)ˆkandˆi+ˆj−2ˆk
View Solution[ˆiˆkˆj]+[ˆkˆjˆi]+[ˆjˆkˆi] is equal to
View Solution[ˆi−ˆjˆj−ˆkˆk−ˆi] is equal to
View SolutionThe value of [ˆi−ˆj,ˆj−ˆk,ˆk−ˆi] is :
View Solution(ˆi+ˆj)×(ˆj+ˆk).(ˆk+ˆi)=
View SolutionFind the shortest distance and the vector equation of the line of shortest distance between the lines given by :
(i)→r=(−4ˆi+4ˆj+ˆk)+λ(ˆi+ˆj−ˆk)
and →r=(−3ˆi−8ˆj−3ˆk)+μ(2ˆi+3ˆj+3ˆk)
(ii)→r=(−ˆi+5ˆj)+λ(−ˆi+ˆj+ˆk)
and →r=(−ˆi−3ˆj+2ˆk)+μ(3ˆi+2ˆj+ˆk).
View SolutionFind the angle between the following pairs of lines :
(i)→r=2ˆi−5ˆj+ˆk+λ(3ˆi+2ˆj+6ˆk) and
→r=7ˆi−6ˆk+μ(ˆi+2ˆj+2ˆk)
(ii) →r=3ˆi+ˆj−2ˆk+λ(ˆi−ˆj−2ˆk) and
→r=2ˆi−ˆj−56ˆk+μ(3ˆi−5ˆj−4ˆk).
View Solution
