समान द्रव्यमान m के छः बिन्दु द्रव्यमान, l भुजा वाले समषट्कोण के शीर्ष पर स्थित हैं। इनमें से किसी भी द्रव्यमान पर कार्यरत बल है-

A

$\frac{G m^{2}}{l^{2}} [\frac{5}{4} + \frac{1}{\sqrt{3}}]$

B

$\frac{G m^{2}}{l^{2}} [\frac{3}{4} + \frac{1}{\sqrt{3}}]$

C

$\frac{G m^{2}}{l^{2}} [\frac{5}{4} - \frac{1}{\sqrt{3}}]$

D

$\frac{G m^{2}}{l^{2}} [\frac{3}{4} - \frac{1}{\sqrt{3}}]$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

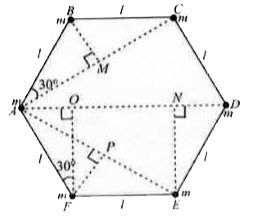चित्र से,
AC=AM+MC=2AM=2l cos $30^{\circ} = 2 l \frac{\sqrt{3}}{2} = \sqrt{3} l$
इसी प्रकार, $A E = \sqrt{3} l$
AD=AO+ON+ND=l sin $30^{\circ}$ +l+sin $30^{\circ}$
$= l \times \frac{1}{2} + l \times \frac{1}{2} = 2 l$
AB=AF=l
B पर द्रव्यमान m के कारण A पर द्रव्यमान m पर बल है -
$F_{A B} = \frac{G m m}{{(A B)}^{2}} = \frac{G m m}{l^{2}}$ AB के अनुदिश
C पर द्रव्यमान m के कारण A पर द्रव्यमान m पर बल है-
$F_{A C} = \frac{G m m}{{(A C)}^{2}} = \frac{G m m}{{(\sqrt{3} l)}^{2}} = \frac{G m^{2}}{3 l^{2}}$ AC के अनुदिश
D पर द्रव्यमान m के कारण A पर द्रव्यमान m पर बल है
$F_{A D} = \frac{G m m}{{(A D)}^{2}} = \frac{G m m}{{(2 l)}^{2}} = \frac{G m^{2}}{4 l^{2}}$ AD के अनुदिश
E पर द्रव्यमान m के कारण A पर द्रव्यमान m पर बल है-
$F_{A E} = \frac{G m m}{{(A E)}^{2}} = \frac{G m m}{{(\sqrt{3} l)}^{2}} = \frac{G m^{2}}{3 l^{2}}$ AE के अनुदिश
F पर द्रव्यमान के कारण A पर द्रव्यमान m पर बल है
$F_{A F} = \frac{G m m}{{(A F)}^{2}} = \frac{G m^{2}}{l^{2}}$ AF के अनुदिश
$F_{A B}$ एवं $F_{A F}$ के कारण परिणामी बल है-
$F_{R_{1}} = \sqrt{F_{A B}^{2} + F_{A B}^{2} + 2 F_{A B} F_{A F} {cos 120}^{\circ}}$
$= \sqrt{{(\frac{{Gm}^{2}}{l^{2}})}^{2} + {(\frac{{Gm}^{2}}{l^{2}})}^{2} + 2 (\frac{{Gm}^{2}}{l^{2}}) (\frac{{Gm}^{2}}{l^{2}}) (- \frac{1}{2})}$
$= \frac{G m^{2}}{l^{2}}$ AD के अनुदिश
$F_{A C}$ एवं $F_{A E}$ के कारण परिणामी बल है-
$F_{R_{2}} = \sqrt{F_{A C}^{2} + F_{A E}^{2} + 2 F_{A C} F_{A E} {cos 60}^{\circ}}$
$= \sqrt{{(\frac{{Gm}^{2}}{{3l}^{2}})}^{2} + {(\frac{{Gm}^{2}}{{3l}^{2}})}^{2} + 2 (\frac{{Gm}^{2}}{{3l}^{2}}) (\frac{{Gm}^{2}}{{3l}^{2}}) (\frac{1}{2})}$
$= \frac{\sqrt{3} G m^{2}}{3 l^{2}} = \frac{G m^{2}}{\sqrt{3} l^{2}}$ AD के अनुदिश
AD के अनुदिश AD के अनुदिश द्रव्यमान m पर नेट बल है-
$F_{R} = F_{R_{1}} + F_{R_{2}} + F_{A D} = \frac{G m^{2}}{l^{2}} + \frac{G m^{2}}{\sqrt{3} l^{2}} + \frac{G m^{2}}{4 l^{2}}$
$= \frac{G m^{2}}{l^{2}} [1 + \frac{1}{\sqrt{3}} + \frac{1}{4}] = \frac{G m^{2}}{l^{2}} [\frac{5}{4} + \frac{1}{\sqrt{3}}]$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

NCERT FINGERTIPS HINDI-गुरुत्वाकर्षण -अभिकथन एवं तर्क प्रारूप प्रश्न

Home
Ask Doubt
Profile