रेखीय आवेश घनत्व $λ$ का वहन करने वाले किसी अनंत बेलन की त्रिज्या $r_{0}$ है। उस बेलन के लिए समविभव पृष्ठ का समीकरण क्या है?

A

$r = r_{o} e^{π ε_{o}} [(V (r) + V (r_{o})] λ$

B

$r = r_{o} e^{2 π ε_{o}} [V (r) - V (r_{o})] λ^{2}$

C

$r = r_{o} e^{- 2 π ε_{o}} [V (r) - V (r_{o})] / λ$

D

$r = r_{o} e^{- 2 π ε_{o}} [V (r) - V (r_{o})] λ$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

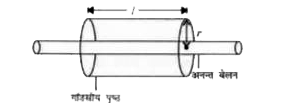
r त्रिज्या एवं l लम्बाई का गाँउसीय पृष्ठ गाउस के प्रमेय के अनुसार
$\oint \vec{E} . \vec{d} s = \frac{q}{ε_{0}} = \frac{λ l}{ε_{0}}$
$E (2 π r l) = \frac{λ l}{ε_{0}}$ या $E = \frac{λ}{2 π ε_{0} r}$ …(i)
$∴ V (r) - V (r_{0}) = - \int_{r_{0}}^{r} \vec{E} . \vec{d} l = \frac{λ}{2 π ε_{0}} \frac{\log_{e} r_{0}}{r}$
दिये गये V(r) के समविभव पृष्ठ के लिए,
$\frac{\log_{e} r}{r_{0}} = \frac{2 π ε_{0}}{λ} [V (r) - V (r_{0})]$
$∴ r = r_{0} e^{- 2 π ε_{0}} [V (r) - V (r_{0})] / λ$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

NCERT FINGERTIPS HINDI-स्थिरवैद्युत विभव तथा धारिता -बहुविकल्प प्रश्न पिटारा (चालकों का स्थिरवैद्युत)

Home
Ask Doubt
Profile