Two vectors →P and →Q are having their magnitudes in the ratio √3:1.Further।→P+→Q।=।→P−→Q। then the angle between the vectors (→P+→Q) and (→P−→Q) isSolution in Telugu
60∘
Topper's Solved these Questions
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - NUMERICAL EXXERCISE (LEVEL -1)
12 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
6 Videos
Similar Questions
Find the components of vector ¯¯¯A=2ˆi+3ˆj along the directions of ˆi+ˆjandˆi−ˆj
View SolutionA body of mass 5Kg moves under a force of 10ˆi+15ˆj−20ˆk . What is the acceleration produced?
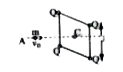
View SolutionFour identical point charges are fixed at the four corners of a square of a side length l. Another charged particle of mass m and charge +q is projected towards centre of square from a large, distance along the line perpendicular to plane of square. The minimum value of initial velocity V0 in m/s required to cross the square is? (m=1gm.l=4√2m,Q=1μc,q=0.5μc)
View SolutionA fish is at a depth of 12 cm in water is viewed by an observer on the bank of a lake. To what height the image of the fish is raised in cm ?
View SolutionIf vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
View SolutionIf |vecP + vecQ|= | vecP| -|vecQ| , the angle between the vectors vecP and vecQ is
View Solutionif |vecP + vecQ| = |vecP| + |vecQ| , the angle between the vectors vecP and vecQ is
View SolutionIf |vecP + vecQ| = |vecP -vecQ| the angle between vecP and vecQ is
View Solutionif vecP +vecQ = vecP -vecQ , then
View SolutionMagnitude of resultant of two vectors vecP and vecQ is equal to magnitude of vecP . Find the angle between vecQ and resultant of vec2P and vecQ .
View SolutionIf |vecP+vecQ|=|vecP|+|vecQ| . The angle between the vectors vecPandvecQ is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P∣∣−∣∣→Q∣∣, the the angle between the vectors →Pand→Q
View SolutionThere vectors vecP, vecQ and vecR are such that vecP+vecQ+vecR=0 Vectors vecP and vecQ are equal in , magnitude . The magnitude of vector vecR is sqrt2 times the magnitude of either vecP or vecQ . Calculate the angle between these vectors .
View Solution→P+→Q=→P−→Q है
View SolutionMagnitude of resultant of two vectors vecP and vecQ is equal to magnitude of vecP . Find the angle between vecQ and resultant of vec2P and vecQ .
View Solution
