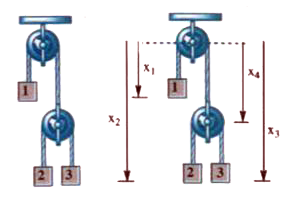
Find the constraint relation between a1,a2anda3.
Points 1,2,3 and 4 are movable. Let their dis-placements from a fixed line be x1,x2,x3andx4
We have x1+x4=l1 ( length of first string ) ..... (i)
and (x2−x4)+(x3−x4)=l2 (length of second string )
or x2+x3−2x4=l2............ (ii)
On double ,differentiating with respect to time ,
we get a1+a4=0 ............ (iii)
and a2+a3−2a4=0 ......... (iv)
But since a4=−a1a4=−a1 [From equation (iii) ]
we have ,a2+a3+2a1=0
This is the required constraint relation between a1,a2anda3
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:LONG ANSWER TYPE QUESTIONS
Explore 4 Videos
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:SHORT ANSWER TYPE QUESTION
Explore 5 Videos
- GEOMETRICAL OPTICSBook:AAKASH SERIESChapter:GEOMETRICAL OPTICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 6 Videos
- LOGIC GATESBook:AAKASH SERIESChapter:LOGIC GATESExercise:Exercise (Very Short Answer)
Explore 16 Videos
Similar Questions
Three rectangles A1, A2 and A3 have the same area. Their lengths a1, a2 and a3 respectively are such that a1<a2<a3 . Cylinders C1, C2 and C3 are formed from A1, A2 and A3 respectively by joining the parallel sides along the breadth. Then C1 will enclosed maximum volume (b) C2 will enclosed maximum volume (c) C3 will enclosed maximum volume (d) Each of C1, C2 and C3 will enclose equal volume
View SolutionIf (b2−b1)(b3−b1)+(a2−a1)(a3−a1)=0, then prove that the circumcenter of the triangle having vertices (a1,b1),(a2,b2) and (a3,b3) is (a2+a32,b2+b32).
View SolutionIf (b2−b1)(b3−b−1)+(a2−a1)(a3−a1)=0, then prove that the circumcenter of the triangle having vertices (a1,b1),(a2,b2) and (a3,b3) is (a2+a32,b2+b32).
View SolutionThe equation Ax−a1+A2x−a2+A3x−a3=0whereA1,A2,A3>0anda1<a2<a3 has two real roots lying in the invervals. (A) (a1,a2)and(a2,a3) (B) (−∞,a1)and(a3,∞) (C) (A1,A3)and(A2,A3) (D) none of these
View SolutionThe equation Ax−a1+A2x−a2+A3x−a3=0,whereA1,A2,A3>0anda1<a2<a3 has two real roots lying in the invervals.
(A) (a1,a2)and(a2,a3) (B) (−∞,a1)and(a3,∞) (C) (A1,A3)and(A2,A3) (D) none of these
View SolutionIf a1,a2,a3,...a20 are A.M's inserted between 13 and 67 then the maximum value of the product a1a2a3...a20 is
View SolutionFOr an integer n<2, we have real numbers a1,a2,a3,a4,..........,an such that a2+a3+a4+.......+an=a1anda1+a3+a4+...........+an=a2...............a1+a2+a3+..............+an−1=an what is the value of a1+a2+a3+........+an?
View SolutionIf a1+a2+a3+......+an=1∀a1>0,i=1,2,3,......,n, then find the maximum value of a1a2a3a4a5......an.
View SolutionFind the coefficient of x in the determinant ∣∣ ∣ ∣∣(1+x)a1b1(1+x)a1b2(1+x)a1b3(1+x)a2b2(1+x)a2b2(1+x)a2b3(1+x)a3b3(1+x)a3b2(1+x)a3b3∣∣ ∣ ∣∣=0.
View SolutionIf A1,A2,A3,,........A51 are arithmetic means inserted between the numbers a and b, then find the value of (b+A51b−A51)−(A1+aA1−a)
View Solution
