Using constraint equations find the relation between a1anda2

Text Solution
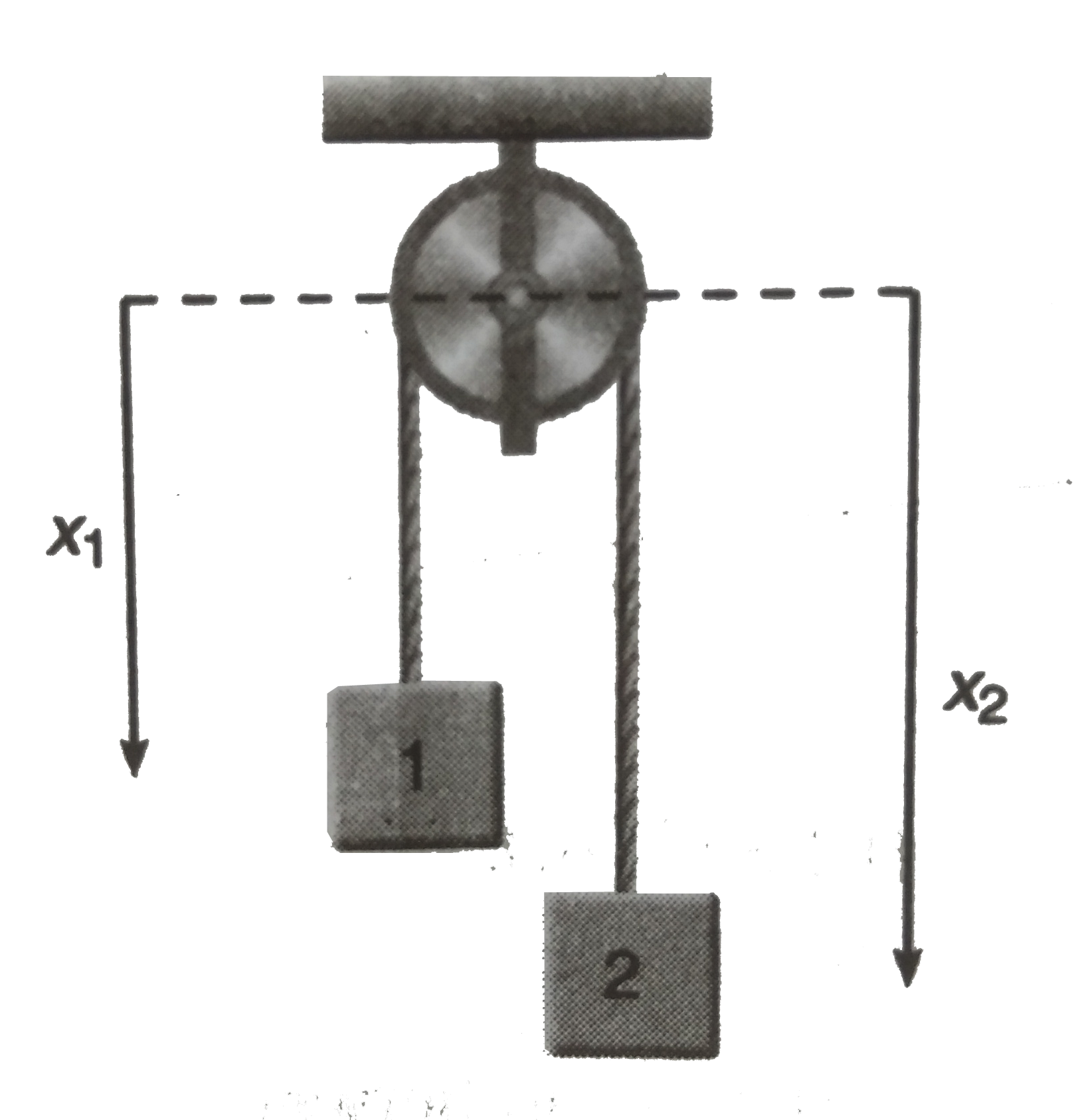
Point 1,2,3 and 4 are movable. Let their dis-placement from a fixed line be x1,x2,x3andx4
x1+x3=l1
(x1−x3)+(x4−x3)=l2
(x1−x4)+(x2−x4)=l3
On double differentiating with respect to time ,
we will get following three constraint relations :
a1+a3=0 ....... (i)
a1+a4−2a3=0........ (ii)
a1+a2−2a4=0............ (iii)
Solving Eqs. (i) ,(ii) and (iii) , we get a2=−7a1
Which is the desired relation between a1anda2

|
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:LONG ANSWER TYPE QUESTIONS
Explore 4 Videos
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:SHORT ANSWER TYPE QUESTION
Explore 5 Videos
- GEOMETRICAL OPTICSBook:AAKASH SERIESChapter:GEOMETRICAL OPTICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 6 Videos
- LOGIC GATESBook:AAKASH SERIESChapter:LOGIC GATESExercise:Exercise (Very Short Answer)
Explore 16 Videos
Similar Questions
Knowledge Check
Two AMs.A1 and A2, two GMs. G1 and G2 and two HMs. H1 and H2 are inserted between any two numbers. Then find the arithmetic mean between H1 and H2 in terms of A1,A2,G1,G2.
AA1+A22G1G2BA1−A22G1G2CA1+A22+G1G2DG1+G22A1A2If the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b2+b2)y+c=0, then the value of C is
Aa21−a22+b21−b22B√a21+b21−a22−b22C12(a21+a22+b21+b22)D12(a21+b22+a21+b22)Two concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
Aq1=4πε0(ϕ1−ϕ2a2−a1)a1a2Bq1=4πε0(ϕ1+ϕ2a2+a1)a1a2Cq1=πε0(ϕ1−ϕ2a2+a1)a1a2Dq1=2πε0(ϕ1+ϕ2a2−a1)a1a2
Using constraint method find the relation between accelerations of 1 and 2.
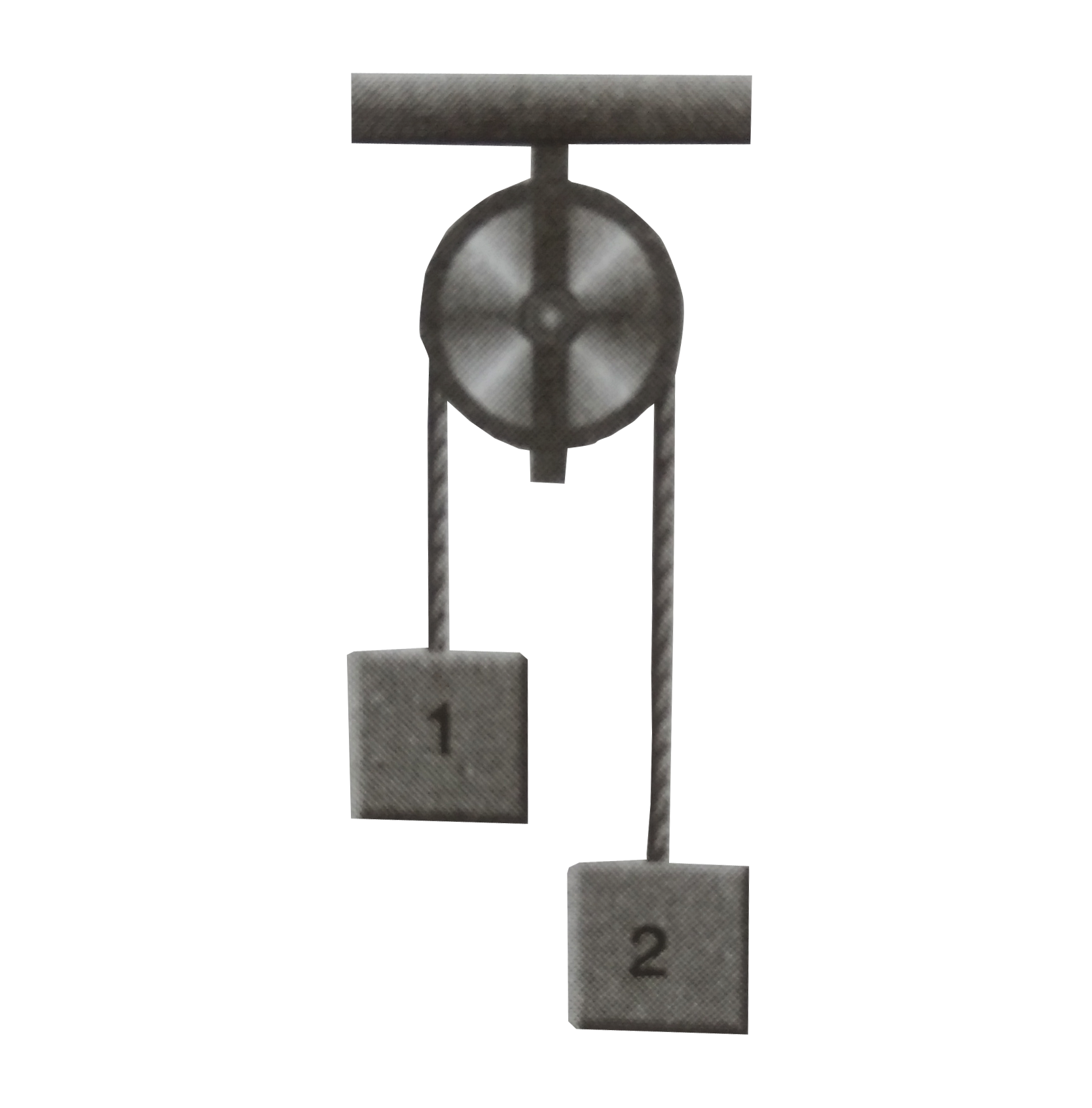
View SolutionUsing constraint method find the relation between accelerations of 1 and 2.

View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0 , then the value of c is aa2−a22+b12−b22 √a12+b12−a22−b22 12(a12+a22+b12+b22) 12(a22+b22−a12−b12)
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0 , then find the value of c.
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b2+b2)y+c=0, then the value of C is
View Solution

