A vector √3ˆi+ˆj rotates about its fail through an angle 300 in clock wise direction then the new vector is
The magnitude of √3ˆi+ˆj is √3+1=2 the angle made by the vector with x-axis is
tanθ=AyAx=1√3
∴θ=30∘
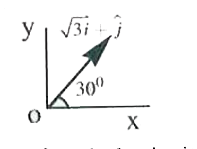
When the given vector rotates 30 in clock wise its direction changes along x - axis but its magnitude does not change.
∴ The new vetor is 2ˆi

Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - PROBLEMS (LEVEL-II)
13 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
Knowledge Check
A vector ˆi+√3ˆj rotates about its tail through an angle 60∘ in clockwise direction then the new vector is
Aˆi+√3ˆjB3ˆi−4ˆjC2ˆjD2ˆiThe axes of coordinates are rotated about the z-axis though an angle of π/4 in the anticlockwise direction and the components of a vector are 2√2, 3√2,4. Prove that the components of the same vector in the original system are -1,5,4.
A5,−1,4B5,−1,4√2C−1,−5,4√2D−1,5,4Find a unit vector →c if −ˆi+ˆj−ˆk bisects the angle between vectors →c and 3ˆi+4ˆj.
A115(11ˆi+10ˆi+2ˆk)B−115(11ˆi−10ˆi+2ˆk)C−115(11ˆi−10ˆi−2ˆk)D−115(11ˆi+10ˆi+2ˆk)
A vector 4ˆi+3ˆj rotates about its tail through an angle 53∘ in anticlockwise direction then the new vector is
View SolutionA vector 3i + 4j rotates about its tail through an angle 37° in anticlockwise direction then the new vector is
View SolutionThe position vector of A is p¯i+¯j.If A is rotated about O through an angle π6 in anti clock wise direction. It coincides with B whose position vector ¯i+q¯j.The value of p,q are
View SolutionLet a vector aˆi+βˆj be obtained by rotating the vector √3ˆi+ˆj by an angle 45∘ about the origin in counterclockwise direction in the first quadrant. Then the area of triangle having vertices (α,β),(0,β)and(0,0) is equal to:
View SolutionA vector →A is rotated through angle θ about its tail. Change of position vector of its tip of is:
View Solution
