A beam of parallel rays of width b cm propagates in glass at an angle θ to its plane face. What would the beam width b1 be after it goes over to air thrugh this face? (The refractive index of the glass is μ)
bμ
bμcosθ
b(1−μ2cos2θ)1/2sinθ
b(1−μ2sin2θ)1/2cosθ
The correct Answer is:C
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
1 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
21 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
98 Videos
Similar Questions
A beam of parallel rays of width b propagates in glass at an angleθto its plane face .The beam width after it goes over to air through this faceis…….if the refractive index of glass is μ.v
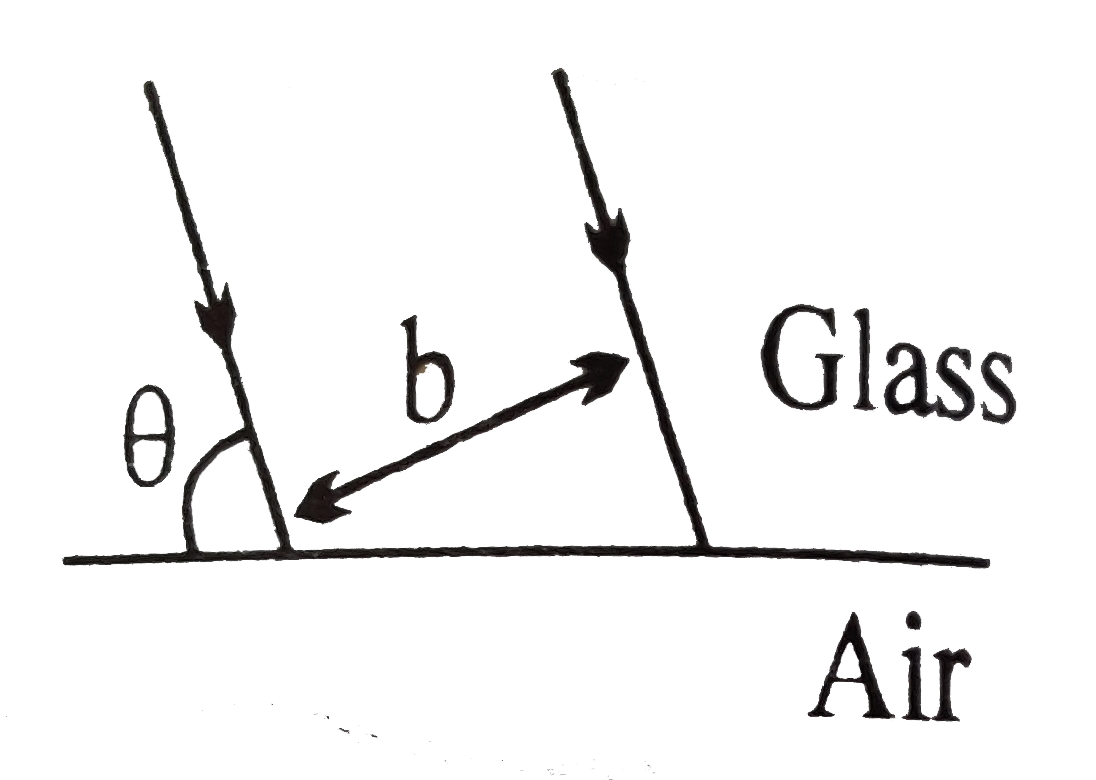
View SolutionA beam of parallel rays of diameter 'b' propagates in glass at an angle θ to its plane. Find the diameter of the beam when it goes to air through this face. (nglass=n)
View Solution
Knowledge Check
A paralel beam of monochromatic light is incident on a glass slab at an angle of incidentce 45∘. Find the ratio of width of beam in glass to that in air ( If refractive index of glass is 1.5).
A11.2475B11.4134C11.732D1On a glass plate, a light beam is incident at an angle of 60∘. If the reflected and the refracted rays are mutually perpendicular, the refractive index of glass is
A√32B√3C32D1√3The angles of incidence and refraction of a monochromatic ray of light of wavelength λ at an air-glass interface are i and r, respectively. A parallel beam of light with a small spread δλ in wavelength about a mean wavelength λ is refracted at the same air-glass interface. The refractive index μ of glass depends on the wavelength λ as μ(λ)=a+b/λ2 where a and b are constants. Then the angular spread in the angle of refraction of the beam is
A∣∣∣siniλ3cosrδλ∣∣∣B∣∣∣2bλ3δλ∣∣∣C∣∣∣2btanraλ3+bλδλ∣∣∣D∣∣ ∣∣2b(a+b/λ2)siniλ3δλ∣∣ ∣∣
A beam of parallel rays of diameter 'b' propagates in glass at an angle θ to its plane. Find the diameter of the beam when it goes to air through this face. (nglass=n)
View SolutionA parallel beam of monochromatic light is incident on a glass slab at an angle of incidence 60∘. Find the ratio of width of the beam in the glass to that in the air if refractive index of glass is 3/2.
View SolutionThe angles of incidence and refraction of a monochromatic ray of light of wavelength λ at an air-glass interface are i and r, respectively. A parallel beam of light with a small spread δλ in wavelength about a mean wavelength λ is refracted at the same air-glass interface. The refractive index μ of glass depends on the wavelength λ as μ(λ)=a+b/λ2 where a and b are constants. Then the angular spread in the angle of refraction of the beam is
View SolutionA parallel beam of monochromatic light is incident on a glass slab at an angle of 35∘. The ratio of width of beam in glass to that in air is [ μg=1.5]
View SolutionA ray of light is incident on a medium of refractive index √2 at an angle of incidence of 45∘. The ratio of the width of the incident beam in air to that of the refracted beam in the medium is
View Solution
