Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.Solution in Kannada
The correct Answer is:4 sq. units.
Step by step video, text & image solution for Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - TEXTUAL EXERCISE EXERCISE 7.4
8 Videos
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - MULTIPLE CHOICE QUESTIONS
11 Videos
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - TEXTUAL EXERCISE EXERCISE 7.2
10 Videos
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)
9 Videos
- CONSTRUCTIONSBOOK - ZEN PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOTS [HIGHER ORDER THINKING SKILLS] - QUESTIONS) IIT /OLYMPIAD/ IMO
5 Videos
Similar Questions
Determine the ratio in which the line 2x + y - 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).

View SolutionThe distance between (a cos θ + b sin θ,0) and (0,a sin θ−bcosθ) is
View SolutionFind the corrdinates of the point which divides the join of (-1, 7) and (4, -3) into the ratio 2 : 3 internally.
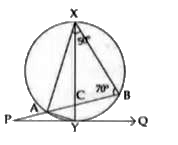
View SolutionIn the adjoining figure, XY is a diameter of the circle and PQ is a tangent to the circle at Y. Given that ⌊AXB=50∘ and ⌊ABX=70∘, calculate ⌊BAY and ⌊APY.
View SolutionGiven below are the steps of construction of a pair of tangents to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm. Find which of the following steps is wrong.
(P) Step 1: Take a point O on the plane paper and draw a circle of radius OA = 4 cm. Also draw a concentric circle of radius OB = 6 cm.
(Q) Step 2: Find the midpoint C of OB and draw a circle of radius BA= AO. Suppose this circle intersects the circle of radius 4 cm at P and Q.
(R) Step 3: Join BP and BQ to get the desired tangents.
View SolutionFind the area of the triangle formed by joining the mid–points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by the mid points of sides of the triangle whose vertices are (2,1),1-2,3),(4,-3)
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0,−1),(2,1)and(0,3). Find the ratio of this area to the area of the given triangle.
View Solutionशीर्षो (0, -1), (2, 1) और (0, 3) वाले त्रिभुज की भुजाओ के मध्य-बिन्दुओ से बनने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए । इस क्षेत्रफल का दिए हुए त्रिभुज के क्षेत्रफल के साथ अनुपात ज्ञात कीजिए ।
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are ( 0 , - 1) , ( 2 , 1) and ( 0 , 3) . Find the ratio of this area to the area of the given triangle . (AS1)
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View Solutionशीर्षो (0,-1),(2,1) और (0,3) वाले त्रिभुज की भुजाओं के मध्य-बिंदुओं से बनाने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए। इस क्षेत्रफल का दिए हुए त्रिभुज के क्षेत्रफल के साथ अनुपात ज्ञात कीजिए।
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle, whose vertices are (2, - 4), (6, 2) and (- 4, 6). Find the ratio of this area to the area of the given triangle.
View Solution
