The ratio in which the line segment $(a_{1}, b_{1})$ and B $(a_{2}, b_{2})$ is divided by Y-axis is Solution in Kannada

$- a_{1} : a_{2}$

$a_{1} : a_{2}$

$b_{1} : b_{2}$

$- b_{1} : b_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B

Updated on:21/07/2023

Answer

Step by step video, text & image solution for The ratio in which the line segment (a_(1), b_(1)) and B(a_(2), b_(2)) is divided by Y-axis is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS COORDINATE GEOMETRY

Topper's Solved these Questions

CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - VERY SHORT ANSWER [VSA] TYPE QUESTIONS
14 Videos
CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - SHORT ANSWER [SA] TYPE QUESTIONS
57 Videos
CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - TEXTUAL EXERCISE EXERCISE 7.4
8 Videos
CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)
9 Videos
CONSTRUCTIONSBOOK - ZEN PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOTS [HIGHER ORDER THINKING SKILLS] - QUESTIONS) IIT /OLYMPIAD/ IMO
5 Videos

Similar Questions

Find the area of the triangle $Δ$ ABC with A(a,b+c), B(b,c+a), and C(c, a+ b).
View Solution
Find the value (s) of x if distance between A (0, 0) and B (x,-4) is 5 units.
View Solution
Determine the ratio in which the line 2x + y - 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).

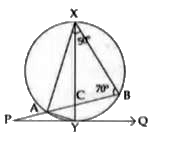
View Solution
In the adjoining figure, XY is a diameter of the circle and PQ is a tangent to the circle at Y. Given that $⌊ A X B = 50^{\circ}$ and $⌊ A B X = 70^{\circ}$ , calculate $⌊ B A Y$ and $⌊ A P Y$ .

View Solution
Given below are the steps of construction of a pair of tangents to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm. Find which of the following steps is wrong.
(P) Step 1: Take a point O on the plane paper and draw a circle of radius OA = 4 cm. Also draw a concentric circle of radius OB = 6 cm.
(Q) Step 2: Find the midpoint C of OB and draw a circle of radius BA= AO. Suppose this circle intersects the circle of radius 4 cm at P and Q.
(R) Step 3: Join BP and BQ to get the desired tangents.
View Solution
det[[2a_(1)b_(1),a_(1)b_(2)+a_(2)b_(1),a_(1)b_(3)+a_(3)b_(1)a_(1)b_(2)+a_(2)b_(1),2a_(2)b_(2),a_(2)b_(3)+a_(3)b_(2)a_(1)b_(3)+a_(3)b_(1),a_(3)b_(2)+a_(2)b_(3),2a_(3)b_(3)]]=
View Solution
The ratio in which the line segment joining points $A (a_{1}, b_{1})$ and $B (a_{2}, b_{2})$ is divided by y-axis is $a_{1} : a_{2}$ (b) $a_{1} : a_{2}$ (c) $b_{1} : b_{2}$ (d) $- b_{1} : b_{2}$
View Solution
If the equation (a_(1)-a_(2))x+(b_(1)-b_(2))y=c represents the perpendicular bisector of the segment joining (a_(1),b_(1))(a_(2),b_(2)), then 2c=
View Solution
If the points $(a_{1}, b_{1}) m (a_{2}, b_{2}) and (a_{1} - a_{2}, b_{2} - b_{2})$ are collinear, then prove that $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}$
View Solution
If a,b are positive quantitis and if $a_{1} = \frac{a + b}{2}, b_{1} = \sqrt{a_{1} b}, a_{2} = \frac{a_{1} + b_{1}}{2}, b_{2} = \sqrt{a_{2} b_{1}}$ and so on then
View Solution
यदि बिंदु $(a_{1}, b_{1}), (a_{2}, b_{2})$ और $(a_{1} - a_{2}, b_{1} - b_{2})$ संरेख है तो सिद्ध कीजिए कि $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}$
View Solution
बिन्दुओं $A (a_{1}, b_{1})$ तथा $B (a_{2}, b_{2})$ को मिलाने वाली रेखाखण्ड को y-अक्ष जिस अनुपात में विभाजित करती है, वह अनुपात है :
View Solution
यदि बिंदु $(a_{1}, b_{1}), (a_{2}, b_{2})$ और $(a_{1} + a_{2}, b_{1} + b_{2})$ संरेख हैं, तो दर्शाइए कि : $a_{1} b_{2} = a_{2} b_{1}$
View Solution
The ratio in which the x-axis divides the line segment joining the points $A (a_{1}, b_{1})$ and $B (a_{2}, b_{2})$ is
View Solution
$Δ = ∣ ∣ ∣ \begin{matrix} a_{1} & b_{1} a_{2} & b_{2} \end{matrix} ∣ ∣ ∣$ and $A_{1}, B_{1}, A_{2}, B_{2}$ are cofactor of $a_{1}, b_{1}, a_{2}, b_{2}$ respectively then , $∣ ∣ ∣ \begin{matrix} A_{1} & B_{1} A_{2} & B_{2} \end{matrix} ∣ ∣ ∣$ has value equal to
View Solution

ZEN PUBLICATION-CO-ORDINATE GEOMETRY-ZEN ADDITIONAL QUESTIONS - MULTIPLE CHOICE QUESTIONS

The distance between (a cos theta + b sin theta,0) and (0,a sin theta ...
03:21
The co ordinates of the point which is reflection of the point (-3, 5)...
01:57
If point P(6,2) divides the line joining A (6,5) and B (4, y) in the r...
01:57
The ratio in which the line segment (a(1), b(1)) and B(a(2), b(2)) is ...
02:21
The length of the line segment joining A(2,3) and B is 10 units . If a...
02:57
If the centroid of a triangle formed by the points a. b), (b, c), and ...
04:01
The coordinates of a point on the X-axis which lie on theL bisector of...
06:02
If (t, 2t), (-2, 6), and (3, 1) are collinear, t =
02:33
Length of the median through C of Delta ABC with A(4,9) B(2, 3), and C...
03:05
If P(2, 4), Q(0, 3), R(3, 6), and S(5, y) are the vertices of a parall...
03:37
The distance between the origin and co-ordinates of point (x,y) is
01:07

Home
Ask Doubt
Profile

The ratio in which the line segment ( a 1 , b 1 ) and B ( a 2 , b 2 ) is divided by Y-axis is Solution in Kannada

The correct Answer is:A, B

Topper's Solved these Questions

Similar Questions

ZEN PUBLICATION-CO-ORDINATE GEOMETRY-ZEN ADDITIONAL QUESTIONS - MULTIPLE CHOICE QUESTIONS

The ratio in which the line segment $(a_{1}, b_{1})$ and B $(a_{2}, b_{2})$ is divided by Y-axis is Solution in Kannada