दो गेंदों के रेखिक संवेग तथा है जो मुक्त आकाश में संघट्ट करती है गेंदों पर कोई बाह्य बल कार्यरत नहीं है। माना तथा इनके अंतिम संवेग है। निम्न विकल्पों में से कौन से विकल्प p, तथा के किसी भी अशून्य मान के लिए मान्य नहीं है (है )
The correct Answer is:A, D
सभी तीनो दिशाओ में निकाय का प्रारंभिक संवेग शून्य है।
और इसलिए रेखीय संवेग संरक्षण के नियमानुसार संघट्ट के पश्चात शून्य होना चाहिए।
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - कार्य, ऊर्जा, शक्ति एवं संघट्ट EXERCISE - JEE SECTION (REASONING TYPE QUESTIONS)6videos
कार्य, ऊर्जा, शक्ति एवं संघट्ट
- BOOK - ERRORLESS HINDICHAPTER - कार्य, ऊर्जा, शक्ति एवं संघट्ट EXERCISE - JEE SECTION (COMPREHENSION TYPE QUESTIONS)8videos
कार्य, ऊर्जा, शक्ति एवं संघट्ट
- BOOK - ERRORLESS HINDICHAPTER - कार्य, ऊर्जा, शक्ति एवं संघट्ट EXERCISE - GRAPHICAL QUESTIONS13videos
कार्य, ऊर्जा, शक्ति एवं संघट्ट
- BOOK - ERRORLESS HINDICHAPTER - एक विमीय गति EXERCISE - SELF EVALUATION TEST23videos
एक विमीय गति
- BOOK - ERRORLESS HINDICHAPTER - किरण प्रकाशिकीEXERCISE - Self Evaluation Test (किरण प्रकाशिकी)26videos
किरण प्रकाशिकी
Similar Questions
कथन -1 : दो पिण्डो के मध्य प्रत्यास्थ संघट्ट में संघट्ट के बाद पिण्डो की सापेक्ष चाल संघट्ट के पहले पिण्डो की सापेक्ष चाल के बराबर होती है
कथन -2 : प्रत्यास्थ संघट्ट में निकाय का रेखीय सनावेग संरक्षित रहता है02:34View Solutionएक नत समतल के घर्षण रहित पृष्ठ पर M द्रव्यमान का एक छोटा गुटका गतिमान है, बिंदु B पर नत समतल का कोण 60∘से 30∘ अचानक परिवर्तित होता है। गुटका प्रारम्भ में बिंदु A पर विरामावस्था में है। नत समतल तथा गुटके के बिच संघट्ट अप्रत्यास्थ माना गया (g=10मीसे2)
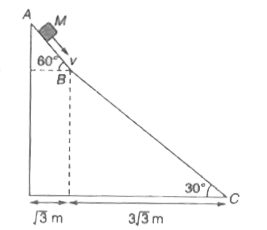
दूसरे नत समतल से टकराने के तुरंत बाद बिंदु B पर गुटके की चाल है02:54View Solutionएक कण मूलबिंदु पर स्थित है तथा इस पर एक बल F = kx कार्यरत है ( जहाँ k एक धनात्मक नियतांक है ) यदि U(0) = 0 हो तब U(x) तथा x के बीच का ग्राफ होगा ( जहाँ U स्थितिज ऊर्जा फलन है )
03:16View Solutionएक कण ऊर्ध्वाधर ऊपर की ओर प्रारम्भिक वेग u से फेंका जाता है। T सैकण्ड के अन्तराल के बाद एक अन्य कण उतने ही वेग u से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है, तो
02:18View Solutionएक खगोलीय दूरदर्शी में सामान्य संजन की स्थिति में, अभिदृश्यक पर एक L लम्बाई की सीधी काली रेखा खींची गई है | नेत्रिका इस रेखा का वास्तविक प्रतिबिम्ब बनाता है | प्रतिबिम्ब की लम्बाई l है | तब दूरदर्शी की आवर्धन क्षमता है
06:52View SolutionLet the vectors →a,→b,→cbe given as a1ˆi+a2ˆj+a3ˆk,b1ˆi+b2ˆj+b3ˆk,c1ˆi+c2ˆj+c3ˆk. Then show that →a×(→b+→c)=→a×→b+→a×→c
08:13View SolutionLet vec b=3hat j+4hat k,vec a=hat i+hat j and let vec b_(1) and vec b_(2) be component of vector b parallel and perpendicular to vec a .If vec b_(1)=(3)/(2)hat i+(3)/(2)hat j then vec b_(2) is equal to
06:21View SolutionLet →a=ˆi+ˆj+ˆk,→b=ˆi and ˆc=c1ˆi+c2ˆj+c3ˆk . Then, (1)If c1=1 and c2=2, find c3 which makes →a,→b and →c coplanar. (2)If c2=−1 and c3=1, show that no value of c1 can make →a,→b and →c coplanar.
08:45View SolutionIf →a=a1ˆi+a2ˆj+a3ˆk;→b=b1ˆi+b2ˆj+b3ˆk,.→c=c1ˆi+c2ˆj+c3ˆk and [3→a+→b 3→b+→c 3→c+→a]=28[→a→b→c] , then find the value of λ4 .
06:47View SolutionTwo balls , having linear momenta vec(p)_(1) = p hat(i) and vec(p)_(2) = - p hat(i) , undergo a collision in free space. There is no external force acting on the balls. Let vec(p)_(1) and vec(p)_(2) , be their final momenta. The following option(s) is (are) NOT ALLOWED for any non -zero value of p , a_(1) , a_(2) , b_(1) , b_(2) , c_(1) and c_(2) (i) vec(p)_(1) = a_(1) hat(i) + b_(1) hat(j) + c_(1) hat(k) , vec(p)_(2) = a_(2) hat(i) + b_(2) hat(j) (ii) vec(p)_(1) = c_(1) vec(k) , vec(p)_(2) = c_(2) hat(k) (iii) vec(p)_(1) = a_(1) hat(i) + b_(1) hat(j) + c_(1) hat(k) ,vec(p)_(2) = a_(2) hat(i) + b_(2) hat(j) - c_(1) hat(k) (iv) vec(p)_(1) = a_(1) hat(i) + b_(1) hat(j) , vec(p)_(2) = a_(2) hat(i) + b_(1) hat(j)
06:06View SolutionIf →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆk and →c=c1ˆi+c2ˆj+c3ˆk prove that →a×(→b+→c)=→a×→b+→a×→c
02:14View SolutionIf ˆi,ˆjandˆk are unit vectors along three mutuaaly perpendicular axes and →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆkand→c=c1ˆi+c2ˆj+c3ˆk prove that
→a.(→b+→c)=→a.→b+→a.→c02:27View SolutionIf ˆi,ˆjandˆk are unit vectors along three mutuaaly perpendicular axes and →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆkand→c=c1ˆi+c2ˆj+c3ˆk prove that
(→b+→c)×→a=→b×→a+→c×→a15:02View Solutionमाना कि △PQR एक त्रिभुज है तथा →a=−−→QR,→b=−−→RP तथा →c=−−→PQ है | यदि |→a|=12,∣∣→b∣∣=4√3 तथा →b.→c=24 तो निम्न में से कोण-सा (से) सही है
02:00View Solutionमाना →U एक ऐसा सदिश है जो सदिशों →a=2ˆi+3ˆj−ˆk तथा →b=ˆj+ˆk के साथ समतलीय है | यदि →U,→a पर लम्बवत है तथा →U⋅→b=24 है, तो ∣∣→U∣∣2 बराबर है :
04:47View Solution

