एक खोखले शंकु को आधार के समांतर किसी समतल द्वारा काटा जाता है और ऊपर के सिरे को हटा दिया जाता है। शेष भाग का वक्र पृष्ठ सम्पूर्ण शंकु के वक्र पृष्ठीय क्षेत्रफल का 89 भाग है । ज्ञात कीजिए की शंकु किस ऊंचाई से काटा गया ?
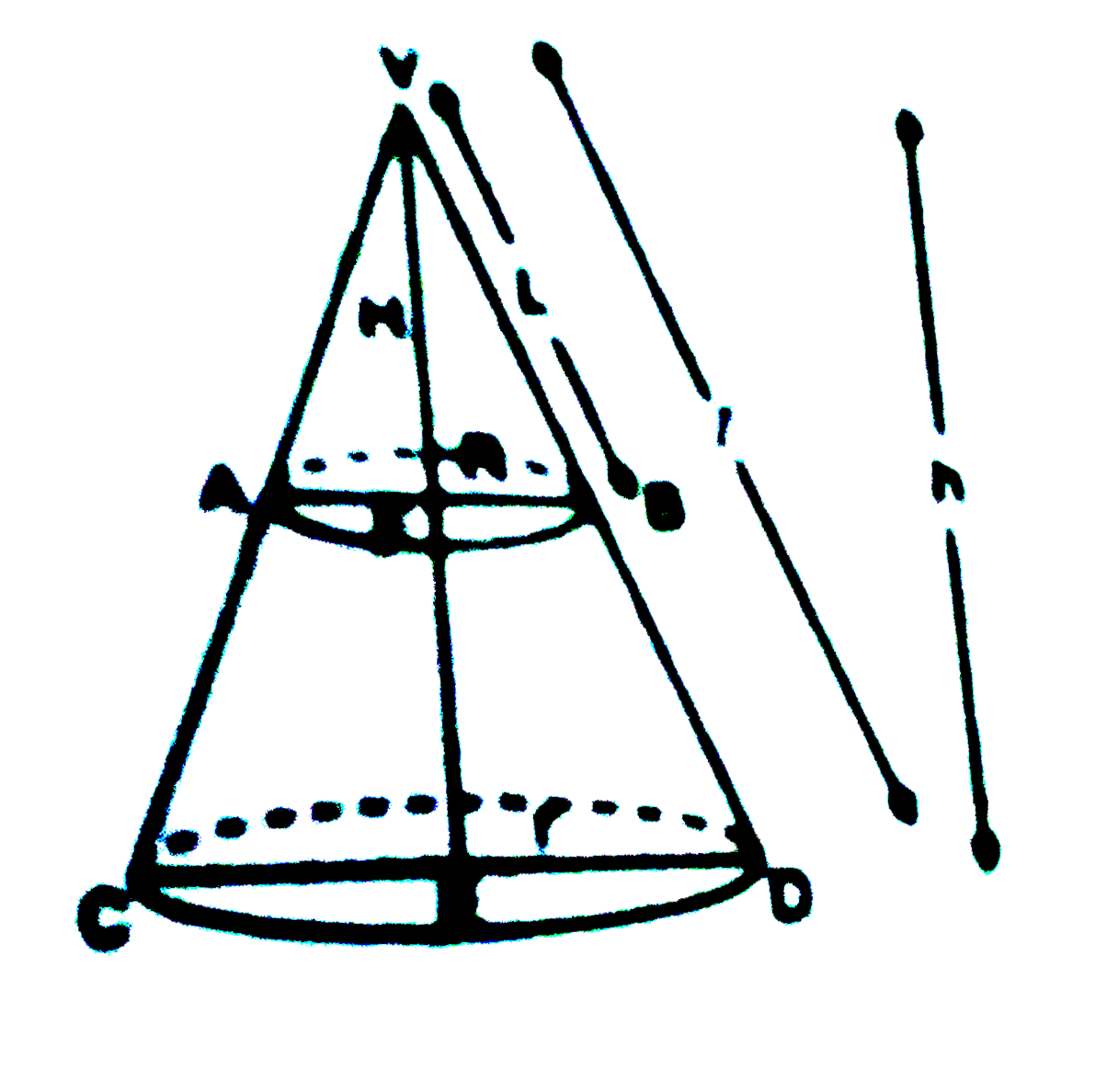
Step by step video & image solution for एक खोखले शंकु को आधार के समांतर किसी समतल द्वारा काटा जाता है और ऊपर के सिरे को हटा दिया जाता है। शेष भाग का वक्र पृष्ठ सम्पूर्ण शंकु के वक्र पृष्ठीय क्षेत्रफल का 8/9 भाग है । ज्ञात कीजिए की शंकु किस ऊंचाई से काटा गया ? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
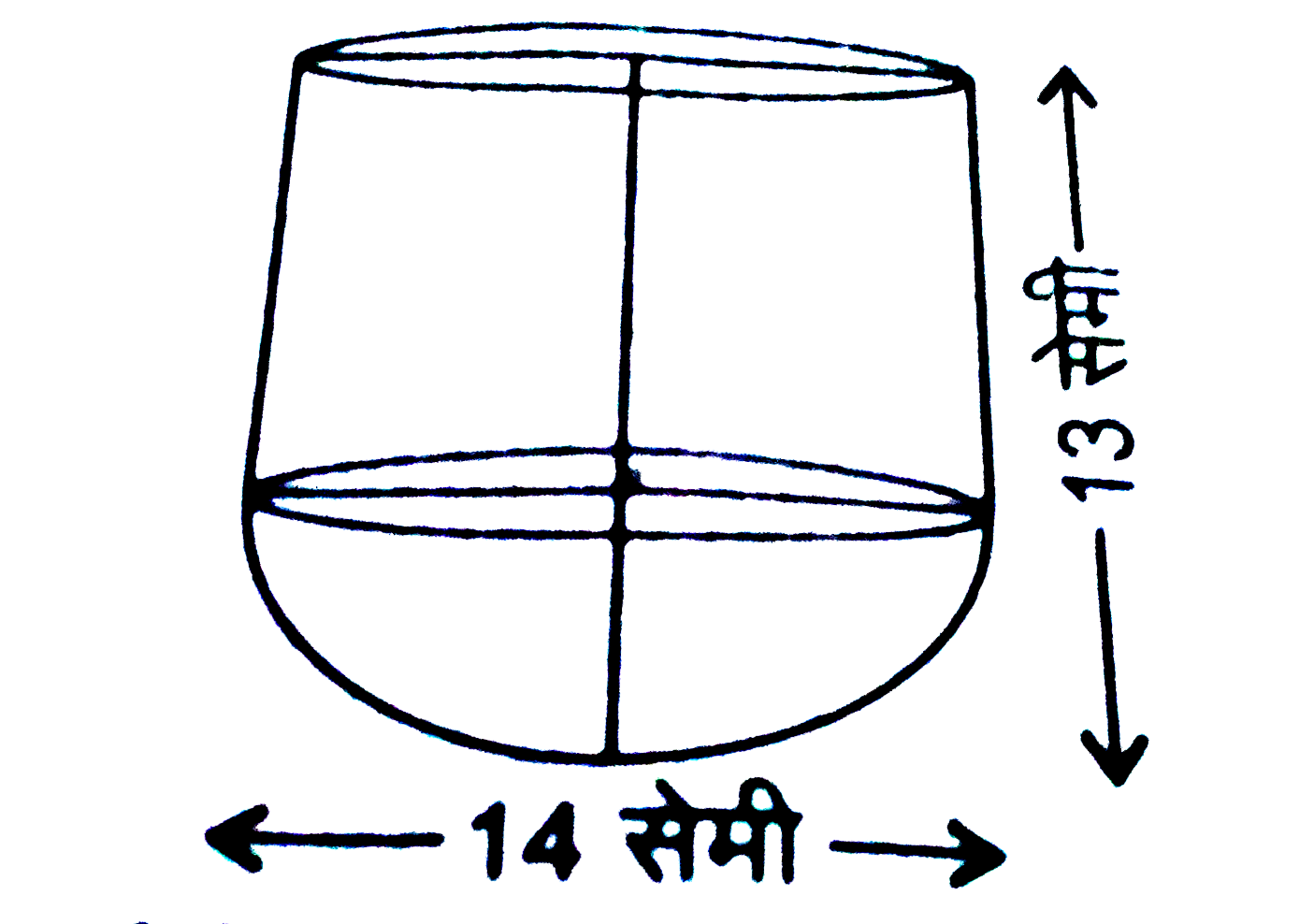
कोई बर्तन एक खोखले अर्द्धगोले के आकार का है किसके ऊपर एक खोखला बेलन अध्यारोपित है जिसके ऊपर एक खोखला बेलन अध्यारोपित है अर्द्धगोले का व्यास 14 सेमी है और इस बर्तन (पात्र) की कुल ऊंचाई 13 सेमी है इस बर्तन का आतंरिक पृष्ठीय ज्ञात कीजिए ।
View Solutionहर के 2m×5n रूप के आधार पर ज्ञात कीजिए कि 14581250 का दशमलव प्रसार कितने स्थानों तक होगा:
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionशंकु का पृष्ठीय क्षेत्रफल|उदाहरण
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का पृष्ठीय क्षेत्रफल#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का पृष्ठीय क्षेत्रफल#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#शंकु के आयतन पर आधारित महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृषठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृष्ठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए महत्वपूर्ण प्रश्न
View SolutionA cube is placed inside a cone of radius 20cm and height 10cm, one of its face being on the base of the cone and vertices of opposite face touching the cone. What is the length (in cm) of side of the cube? एक घन को एक शंकु जिसकी त्रिज्या 20 से. मी. तथा ऊँचाई 10 से.मी. है, के अंदर रखा जाता है, उसको एक सतह शंकु के आधार कौर ओर है तथा विपरीत सतह के शीर्ष शंकु का स्पर्श कर रहे है। घन की भुजा लम्बाई (से. मी. में) क्या है ?
View SolutionFrom a circular sheet of paper of radius 10cm, a sector of area 40% is removed. If the remaining part is used to make a conical surface, then the ratio of the radius and the height of the cone is- किसी कागज की गोलाकार सीट जिसकी त्रिज्या 10 सेमी से वृत्त खंड का 40% हटा दिया जाता है, यदि शेष हिस्से का प्रयोग करके एक शंकु बनाया जाता है, तो शंकु की त्रिज्या तथा ऊँचाई का अनुपात है।
View SolutionA cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8: 5, the ratio of their radius and height is एक बेलन ओर एक शंकु के आधारों की त्रिज्याएँ बराबर है और ऊंचाई बराबर है। यदि उनके वक्र पृष्ठ क्षेत्रफल 8 : 5 के अनुपात में है, तो उनकी त्रिज्या ओर ऊँचाई का अनुपात है-
View SolutionThe volume of a right circular cone is equal to that of a sphere, whose radius is half the radius of the base of the cone. What is the ratio of the radius of the base to the height of the cone ?
एक लम्ब वृत्तीय शंकु का आयतन उस गोले के आयतन के बराबर है, जिसकी त्रिज्या शंकु के आधार की त्रिज्या से आधी है | शंकु के आधार की त्रिज्या और शंकु की ऊंचाई में क्या अनुपात है ?
View SolutionIf the radius of the base of a cone is doubled, and the volume of the new cone is three times the volume of the original cone, then what will be the ratio of the height of the original cone to that of the new cone ?
यदि किसी शंकु के आधार की त्रिज्या दोगुनी कर दी गयी है , और नए शंकु का आयतन आरंभिक शंकु के आयतन का तिगुना है, तो आरंभिक शंकु और नए शंकु की ऊँचाइयों के बीच क्या अनुपात होगा ?
View Solution