एक रैखिक प्रोग्रामन समस्या का उद्देश्य फलन है
The correct Answer is:A
Step by step video & image solution for एक रैखिक प्रोग्रामन समस्या का उद्देश्य फलन है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- रैखिक प्रोग्रामन BOOK - UP BOARD PREVIOUS YEARCHAPTER - रैखिक प्रोग्रामन EXERCISE - दीर्घ उत्तरीय प्रश्न
22 Videos
- रैखिक प्रोग्रामन BOOK - UP BOARD PREVIOUS YEARCHAPTER - रैखिक प्रोग्रामन EXERCISE - बहुविकल्पीय प्रश्नोत्तर
3 Videos
- मॉडल प्रश्न-पत्र-5BOOK - UP BOARD PREVIOUS YEARCHAPTER - मॉडल प्रश्न-पत्र-5EXERCISE - प्रश्न
36 Videos
- संबन्ध एवं फलन BOOK - UP BOARD PREVIOUS YEARCHAPTER - संबन्ध एवं फलन EXERCISE - विस्तृत उत्तरीय प्रश्नोत्तर
7 Videos
Similar Questions
रैखिक प्रोग्रामन समस्या का निम्न अवरोधों के अंतर्गत x+y≤4,x≤0,y≤0 का हल ग्राफीय विधि द्वारा दर्शाया !
View Solutionसंलग्न आकृति में किसी LPP का सुसंगत हल प्रदर्शित है।माना Z=3x−4y उद्देश्य फलन है। Z का न्यूनतम मान किस बिन्दु पर है?
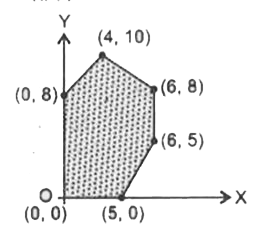
View Solutionसही विकल्प चुनकर अपनी उत्तर पुस्तिका में लिखिए---
समुच्चय (x,y) में द्विआधारी-संक्रियाओं की संख्या है-
View Solutionयदि R और S समुच्ये X में तुल्यता सम्बन्ध हो, तो सिद्ध कीजिए कि R∪S,R∩S, भी X में तुल्यता सम्बन्ध है
View Solutionनिचे दिए गए कथन सत्य है या असत्य ?
किसी रेखीय प्रोग्रामन समस्या के लिए संभाव्य क्षेत्र हमेशा रैखिक बहुभुज होता है।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
कुछ व्यवरोधों(constraints) के अंतर्गत किसी रैखिक फलन का न्यूनतम या अधिकतमीकरण करने की विधि को रैखिक प्रोगामान समस्या कहते हैं। रैखिक फलन को उद्देश्य फलन कहते हैं। रैखिक फलन में ऋणेत्तर चार निहित होते हैं।
View Solutionनिम्न प्रमेय को समझाइए।
प्रमेय 1. यदि एक रैखिक प्रोग्रामन समस्या के लिए R सुसंगत क्षेत्र है तथा उद्देश्य फलन Z=ax+by है। जब Z के एक इष्टतम मान ( अधिकतम या न्यूनतम ) हो जहाँ व्यवरोधों से सम्बंधिर चर और y रैखिक समीकरणों द्वारा व्यक्त हों तब इस इष्टतम मान सुसंगत क्षेत्र के कोनों (शीर्षों )पर होता है।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
रैखिक प्रोग्रामन समस्या को हल करने के लिए निम्न चरण प्रयुक्त होते हैं -
रैखिक प्रोग्रामन का सुसंगत क्षेत्र ज्ञात करके इसके कोनीय बिंदुओं (शीर्ष बिंदुओं ) को ज्ञात करते हैं।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
रैखिक प्रोग्रामन समस्या को हल करने के लिए निम्न चरण प्रयुक्त होते हैं -
सुसंगत क्षेत्र के प्रत्येक कोनीय बिंदु पर उद्देश्य फलन Z=ax+by का मान ज्ञात करते हैं। यहाँ से उद्देश्य का न्यूनतम / अधिकतम मान प्राप्त करते हैं।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionआलेखीय विधि से निम्नलिखित रैखिक प्रोग्रामन समस्या को न्यूनतमीकरण के लिए हल कीजिए :
उद्देश्य फलन Z=5x+y
व्यवरोध 3x+5y≥15
5x+2y≤10
x≥0,y≥0
View Solutionउद्देश्य फलन z=x+2y को अधिकतम करने की समस्या का हल प्रतिबंधों x−y≤2,x+y≤4 तथा x,y≥0 के अंतर्गत है -
View Solutionभूमिका|रेखिक प्रोग्रामन समस्या और उसका गणितीय सूत्रीकरण#!#रेखिक प्रोग्रामन को हल करने की ग्राफीय विधि#!#रेखिक प्रोग्रामन समस्या क भिन्न प्रकार#!#उदाहरण
View Solutionरैखिक प्रोग्रामन समस्या का गणितीय सूत्रीकरण
View Solutionरैखिक प्रोग्रामन समस्या को हल करने की आलेखीय विधि
View Solutionरैखिक प्रोग्रामन समस्या मे परिबद्ध व अपरिबद्ध हल क्षेत्र
View Solution
