A population p(t) of 1000 bacteria introduced into nutrient medium grows according to the relation p(t)=1000+1000t100+t2. The maximum size of this bacterial population is equal to N then sum of the digits in N is
Step by step video & image solution for A population p(t) of 1000 bacteria introduced into nutrient medium grows according to the relation p(t)=1000+(1000t)/(100+t^2). The maximum size of this bacterial population is equal to N then sum of the digits in N is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
A population p(t) of 1000 bacteria introduced intonutrient medium grows according to the relation p(t)=1000+1000t100+t2. The maximum size of the this bacterial population is
View SolutionThe momentum p of a particle changes with the t according to the relation dpdt=(10N)+(2Ns)t. If the momentum is zero at t=0, what will the momentum be at t=10?.
View Solution
Knowledge Check
- Question 1 - Select One
A population p(t) of 1000 bacteria inroduced into nutrient medium grows according to the relation p(t)=1000+1000t100+t2. The maximum size of this bacterial population is
A1100B1250C1050D5250 - Question 2 - Select One
The population p(t) at time t of a certain mouse species follows the differential equation ddtp(t)=0.5p(t)−450. If p(0)=850, then the time at which the population becomes zero is
Alog 9B12log18Clog 18D2 log 18 - Question 3 - Select One
The population p(t) at time t of a certain mouse species follows the differential equation dp(t)dt=0.5 p(t)-450. If p(0)=850, then the time at which the population becomes zero is
A2 ln 18Bln 9C12 ln 18Dln 18
The sum of the first n terms of an A.P. is 3n2+6n . Find the nth term of this A.P.
View SolutionThe population p(t) at a time t of a certain mouse species satisfies the differential equation dp(t)dt=0.5p(t)−450. If p(0)=850. Then the time at which the population becomes zero is
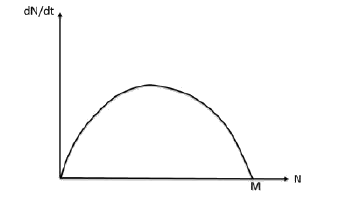
View SolutionIn the graph below. where N is population size and tis time. M represents
 View Solution
View SolutionThe population p(t) at time t of a certain mouse species satisfies the differential equation (dptdt=0.5p(t)−450 If p(0)=850 , then the time at which the population becomes zero is (1) 2 ln 18 (2) ln 9 (3) 12 In 18 (4) ln 18
View SolutionLet the population of rabbits surviving at a time t be governed by the differential equation (dptdt=12p(t)−200. If p(0)=100 , then p(t) equals (1) 400−300et/2 (2) 300−200e−t/2 (3) 600−500et/2 (4) 400−300e−t/2
View Solution
