Show that the products of the corresponding terms of the sequences a, $a r, a r^{2}, ... ... ., a r^{n - 1}$ and $A, A R, A R^{2}, ... ..., A R^{n - 1},$ form a G.P, and find the common ratio.

Video Solution

Text Solution

Verified by Experts

$1^{s t}$ sequence is $a, a r, a r^{2}, ... . . a r^{n - 1}$

$2^{n d}$ sequence is $A, A R, A R^{2}, ... . . A R^{n - 1}$

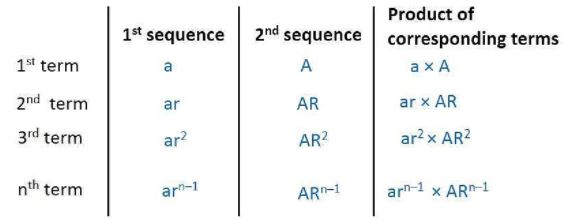
Let $P =$ Product of corresponding terms of $1^{s t}$ and $2^{n d}$ sequence

$P = a \times A, a r \times A R, a r^{2} \times A R^{2}, ... ..., a r^{n - 1} \times A R^{n - 1}$

$P = a A, a r A R, a r^{2} A R^{2}, ... . . a A (r^{n - 1} R^{n - 1})$

Now, in $a A, a r A R, a r^{2} A R^{2}, ... . . a A (r^{n - 1} R^{n - 1})$

$\frac{a r A R}{a A} = r R$

& $\frac{a r^{2} A R^{2}}{a r A R} = R r$

Thus, $\frac{Sec o n d t e r m}{F i r s t t e r m} = \frac{T h i r d t e r m}{Sec o n d t e r m}$ , i.e. common ratio is same

Thus, it is a G.P.

Common ratio= $r = \frac{Sec o n d t e r m}{F i r s t t e r m}$

$r = \frac{a r A R}{a A}$

$r = r R$

|

Updated on:21/07/2023

Class 11 MATHS SEQUENCES AND SERIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If S be the sum, P the product and R the sum of the reciprocals of n terms of a G.P., then ${(\frac{S}{R})}^{n} =$
AP
B $P^{2}$
C $P^{3}$
D $\sqrt{P}$

NCERT-SEQUENCES AND SERIES-EXERCISE 9.3

Home
Ask Doubt
Profile