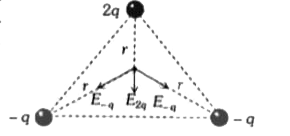
यदि एक समबाहु त्रिभुज के तीनों शीर्ष पर आवेश क्रमशः स्थित हैं , तो त्रिभुज के केन्द्र पर
क्षेत्र शून्य है परन्तु विभव शून्य नहीं है
क्षेत्र शून्य नहीं है परन्तु विभव शून्य है
दोनों क्षेत्र तथा विभव शून्य है
दोनों क्षेत्र तथा विभव शून्य नहीं है
The correct Answer is:B
दिये गये आवेश वितरण के कारण केंद्र पर विद्युत क्षेत्र अशून्य हॉग| 2q आवेश के कारण केंद्र पर विभव
एवं आवेश के कारण
(r = केंद्र की शीर्ष से दुरी)
कुल विभव
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Ordinary Thinking (वैद्युत द्विध्रुव)43videos
स्थिर वैद्युत
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Ordinary Thinking (विद्युत फ्लक्स एवं गॉस नियम)37videos
स्थिर वैद्युत
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Self Evaluation Test8videos
स्थिर वैद्युत
- BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Self Evaluation Test (सरल आवर्त गति )19videos
सरल आवर्त गति
Similar Questions
निरक्षीय समतल में किसी बिन्दु पर द्विध्रव आघूर्ण एवं विद्युत क्षेत्र के बीच कोण होगा
07:55View SolutionR त्रिज्या तथा L लम्बाई के एक बेलन को एकसमान वैद्युत क्षेत्र E के अनुदिश अक्ष में रखा गया है , तो बेलन के पृष्ठ से सम्पूर्ण फ्लक्स हेतु व्यंजक
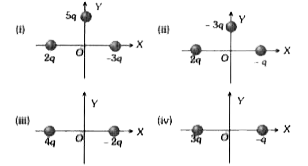
07:05View Solutionनिम्न चार स्थितियों में आवेशित कण मूल बिंदु से बराबर - बराबर दूरियों पर स्थित हैं मूल बिंदु क्षेत्र के परिमाण को अधिकतम पहले लेते हुये इन्हें व्यवस्थित करें
 02:37View Solution
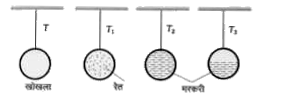
02:37View Solutionएक सरल लोलक , का गोलक एक धात्विक खोकला गोला है। इसका आवर्तकाल T है। जब गोलक में रेत भरी है। तब आवर्तकाल T1 है जब यह मरकरी से भरा है तब आवर्तकाल T2 है जब यह मरकरी से आधा भरा है तब इसका आवर्तकाल T3 है । तब निम्न में से सही विकल्प है।
 06:19View Solution
06:19View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
03:50View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
46:34View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
02:39View Solutionयदि किसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,0),(1,3) और (-1,2) हो तो उसके कोणों को ज्ञात कीजिए।
04:32View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
03:50View Solutionत्रिभुज के आधार पर कुछ महत्वपूर्ण प्रश्न
03:33View Solutionयदि →a,→b तथा →c समबाहु त्रिभुज के शीर्ष के स्थिति सदिश हो जिसका लम्ब केंद्र मूलबिंदु है , तो →a+→b+→c का मान ज्ञात कीजिए।
03:53View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
04:09View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
52:50View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,5), (6,3) और (5,10)47:35View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(1,1), (-1,-1) और (−√3,√3)04:30View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,0), (5,5√3) और (−5,5√3)01:52View Solution

