त्रिज्या R के किसी एक समान आवेशित ठोस गोले के पृष्ठ का विभव V0 है | (∞ के सापेक्ष मापा गया ) | इस गोले के लिये, 3V02,5V02,3V04, तथा V02 विभवों वाले समविभवी पृष्ठों की त्रिज्यायें क्रमशः R1,R2,R3 तथा R4 है | तो
R1=0 तथा R2>(R4−R3)
R1≠0 तथा (R2−R1)>(R4−R3)
R1=0 तथा R2<(R4−R3)
2R<R4
The correct Answer is:C, D

V0=KQR
V(r>R)=KQr
V(r<R)=KQ2R3(3R2−r2)
Vcentre=32KQR=3V02
R2 पर V=5V04=kQ2R3(3R2−R22)
⇒52=3−R22R⇒R2=R√2
R3 पर V=3V04=kQR3⇒R3=43R
R4 पर V=V04=kQR4⇒R4=4R
∴R4−R3=4R−43R=8R3>R2
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - JEE Section (Reasoning type questions)3videos
स्थिर वैद्युत
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - JEE Section (Comprehension type questions)5videos
स्थिर वैद्युत
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Graphical Questions13videos
स्थिर वैद्युत
- BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Self Evaluation Test (सरल आवर्त गति )19videos
सरल आवर्त गति
Similar Questions
कथन -1 : प्रायोगिक उद्देश्यों के लिये विद्युत परिपथ में पृथ्वी को शून्य विभव के आधार स्वरूप माना जाता है |
कथन -2 : त्रिज्या R के गोलीय पृष्ठ पर आवेश Q एकसमान Q वितरित होने पर विद्युत विभव होता है |06:05View Solutionत्रिज्या R के नाभिक में नाभिकीय आवेश ( Ze ) असमान रूप से वितरित है | चित्रानुसार आवेश घनत्व ρ(r), [ प्रति इकाई आयतन आवेश ] नाभिक के केन्द्र से त्रिज्यीय दूरी r पर निर्भर करता है | विद्युत क्षेत्र केवल त्रिज्यीय दिशा के अनुदिश है |
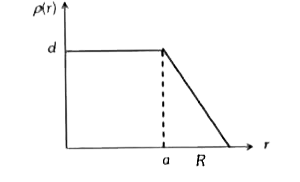
r = R पर विद्युत क्षेत्र है06:09View Solutionदिए गये परिपथ में, C के मान के 1μF से 3μF परिवर्तित होने से, 2μF संधारित्र पर आवेश Q2 में परिवर्तन होता है। के पहलन के रूप में Q2 को कौन-सा आलेख सही दर्शाता है? (आलेख केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं है।)
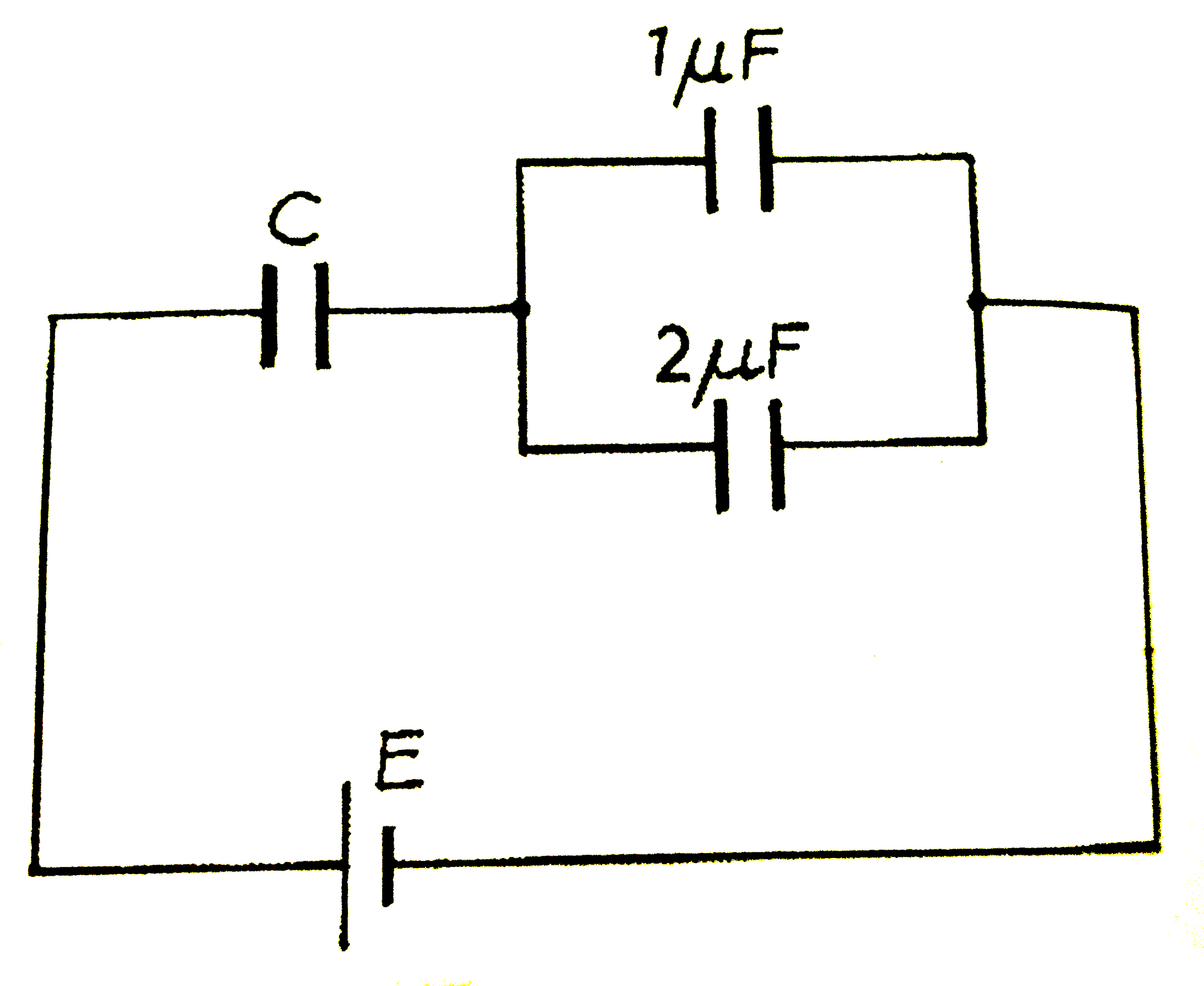 View Solution
View Solutionएक सरल लोलक , का गोलक एक धात्विक खोकला गोला है। इसका आवर्तकाल T है। जब गोलक में रेत भरी है। तब आवर्तकाल T1 है जब यह मरकरी से भरा है तब आवर्तकाल T2 है जब यह मरकरी से आधा भरा है तब इसका आवर्तकाल T3 है । तब निम्न में से सही विकल्प है।
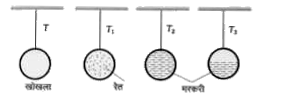 10:27View Solution
10:27View SolutionA uniformly charged solid shpere fo radius R has potential V0 (measured with respect to ∞) on its surface. For this sphere the equipotentail surfaces with potentials 3V02,5V04,3V04 and V04 have radius R1,R2,R3 and R4 respecatively. Then
08:23View Solutionकिसी त्रिभुज के शीर्षो के निर्देशांक (2,5),(6−2) तथा (−3,−4) है , तो उसकी मध्यिकाओ के समीकरण ज्ञात कीजिए
03:50View SolutionDraw a loop ACDBA as -V_(2)+I_(2)R_(1)-I_(1)R_(1)+V_(1)=0.
03:30View SolutionR त्रिज्या के किसी एकसमान आवेशित ठोस गोले के पृष्ठ का विभव V0 है (∞ के सापेक्ष मापा गया)। इस गोले के लिए, 3V02,5V04,3V04 तथा V04 विभवों वाले समविभवी पृष्ठों की त्रिज्याएँ, क्रमशः R1,R2,R3 तथा R4 हैं, तो
02:53View Solutionचित्र में प्रदर्शित जाल के लिये किरचॉफ के नियमों का उपयोग कर सिद्ध कीजिये कि
V0=V[R1R1+R2−R3R3+R4]
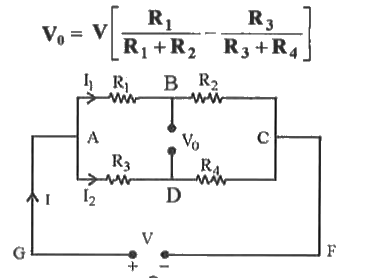 04:06View Solution
04:06View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
03:12View Solutionयदि बिन्दु (4, 2) का रेखा L = 0 के सापेक्ष प्रतिबिम्ब (-2, 6) है, तो L का समीकरण है
04:06View Solutionयदि किसी गोले का समीकरण x2+y2+z2+2ux+2vy+2wz+d=0 है, तो गोले के केन्द्र का निर्देशांक तथा त्रिज्या क्या होगी?
02:40View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
06:55View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
02:13View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
03:52View Solutionगोले 6x2+6y2+6z2−16x+9z−6=0 के केंद्र के निकाय है -
01:21:00View Solution

