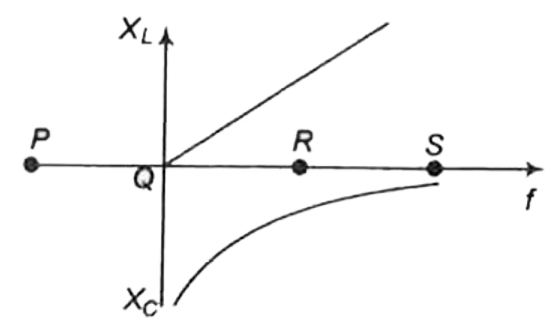
दिये गये XL−f वक्र तथा XC−f के लिए अनुनाद बिंदु है
P
Q
R
S
The correct Answer is:C
अनुनाद की स्थिति में XL=XC
Topper's Solved these Questions
Similar Questions
एक विद्युत द्विध्रुव की एकसमान विद्युत क्षेत्र में स्थितिज ऊर्जा U है। विद्युत क्षेत्र के कारण द्विध्रुव पर आरोपित बल आघूर्ण का मान τ है तब
View Solutionयंग के द्वि-स्लिट प्रयोग में फ्रिन्ज चौड़ाई 0.4 मिमी प्राप्त होती है। यदि पूरे उपकरण को उसकी ज्यामितीय संरचना को बिना परिवर्तित किये 4/3 अपवर्तनांक के पानी में डुबो दिया जाए, तो नई फ्रिन्ज की चौड़ाई होगी
View SolutionIf f(x)=log(1+x1−x),then (a)f(x1)f(x)=f(x1+x2) (b)f(x+2)−2f(x+1)+f(x)=0 (c)f(x)+f(x+1)=f(x2+x) (d)f(x1)+f(x2)=f(x1+x21+x1x2)
View SolutionIf y=f(x) is a curve and if there exists two points A(x_(1),f(x_(1))) and B(x_(2),f(x_(2))) on it such that f'(x_(1))=-(1)/(f(x_(2))), then the tangent at x_(1) is normal at x_(2) for that curve. Now,answer the following questions.
View SolutionIf f(x)=log((1+x)/(1-x)), then f(x) is (i) Even Function (ii) f(x_(1))-f(x_(2))=f(x_(1)+x_(2)) (iii) ((f(x_(1)))/(f(x_(2))))=f(x_(1)-x_(2)) (iv) Odd function
View SolutionThe figure shows variation of R,X_(L) and X_(C) with frequency f in a series L,C,R circuit. Then for what frequency point, the circuit is inductive ?
View SolutionThe resonance point in XL−f and XC−f curves is
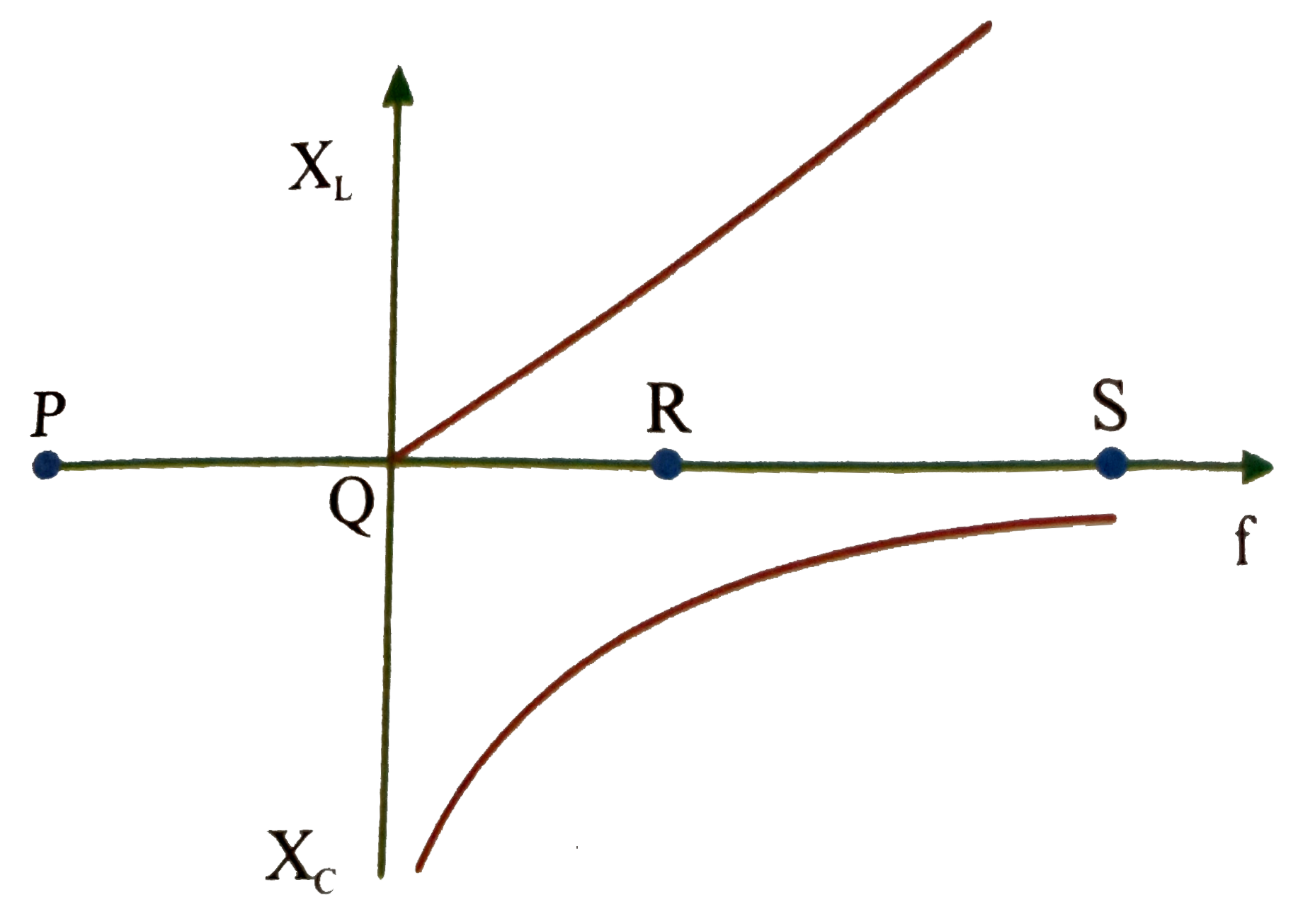
View SolutionIf f(x1−x2),f(x1)f(x2) & f(x1+x2) are in A.P. for all x1,x2 and f(0)≠0 then
View SolutionFor the Booleann function f(x1,x2,x3)=(x1⋅x2)+x3, value of f(1,1,0) is
View Solutionयदि f(x1)=f(x2)⇒x1=x2∀x1,x2∈A, तो फलन f:A→B है
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
View Solutionयदि x1=x2 तो f(x1)=f(x2) तो फलन एकैक होगा|
View Solutionकोई फलन f(x) किसी बिन्दु x2 पर निम्निष्ठ है , तो f''(x2)………..
View Solutionपुनरावृत्ति सूत्र xn+1=xn−f(xn)f'(xn) सामान्य रूप से कहलाता है
View SolutionLet f(x)=[2−x2[2x2]],xεR ( [ ] denotes the greatest integer function). Let x1=0,x2=log23 and x3=√2. Suppose 0<x4<1.
Δ=∣∣ ∣ ∣∣f(x1)f(x2)f(x3)f(x4)f(x4)f(x2)f(x2)f(x3)f(x1)∣∣ ∣ ∣∣ then Δ is equal to
View Solution
