व्यंजक ¯¯¯¯¯¯¯¯¯¯¯A+B.(¯¯¯¯¯¯¯¯A.B) = 1 के लिए A व B के मान होंगे
0,0
0,1
1,0
1,1
The correct Answer is:A
बूलियन व्यंजक को निम्न प्रकार लिखा जा सकता है
Y=(¯¯¯¯¯¯¯¯¯¯¯A+B),(¯¯¯A.B)
=(¯¯¯A.¯¯¯B).(¯¯¯A+¯¯¯B)
(¯¯¯A.¯¯¯A).¯¯¯B+¯¯¯A(¯¯¯B.¯¯¯B)
=(¯¯¯A.¯¯¯B)+¯¯¯A+¯¯¯B
=¯¯¯A.¯¯¯B
अतः सत्यता सारणी है।

Topper's Solved these Questions
- BOOK - ARIHANT HINDICHAPTER - लॉजिक गेट EXERCISE - प्रश्नावली (विगत वषो के प्रश्न)5videos
लॉजिक गेट
- BOOK - ARIHANT HINDICHAPTER - यूनिट टेस्ट 7 (नाभिकीय तथा आधुनिक भौतिकी)EXERCISE - MCQ35videos
यूनिट टेस्ट 7 (नाभिकीय तथा आधुनिक भौतिकी)
- BOOK - ARIHANT HINDICHAPTER - विद्युत चुम्बकीय प्रेरण EXERCISE - प्रश्नावली (विगत वर्षों के प्रश्न)10videos
विद्युत चुम्बकीय प्रेरण
Similar Questions
चित्र में दर्शाये गए चार NAND गेट की सत्य सारणी होगी-
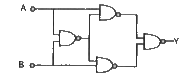 02:26View Solution
02:26View Solutionडेवीसन एवं जर्मन प्रयोग से सिद्ध हुआ
01:56View Solutionएक एकसमान चुम्बकीय क्षेत्र में एक कुण्डली को लटकाया गया है। कुण्डली का तल चुम्बकीय बल रेखाओं के समान्तर है। जब कुण्डली में एक धारा प्रवाहित करते हैं। तब यह दोलन करने लगती है और इसको रोकना मुश्किल हो जाता है। परन्तु जब एक ऐल्युमीनियम प्लेट को कुण्डली के पास लाया जाता है, तब यह रूक जाती है। इसका कारण है
04:03View SolutionWhat will be the input of A and B for the Boolean expression bar((A+B)).bar((A.B))=1 ?
04:54View SolutionWhat will be the input A and B for the Boolean expression (bar(A+B)).(bar(A.B)) =1 ?
04:13View Solutionदर्शाइए कि दो शून्येतर सदिशों ¯a और ¯b के लिए,
|¯a|¯b+∣∣¯b∣∣¯a,|¯a|¯b−∣∣¯b∣∣¯a पर लम्ब है |04:01View Solutionकिन्हीं दो शून्येतर सदिशों के लिए, सिद्ध कीजिए कि
∣∣¯a+¯b∣∣2+∣∣¯a−¯b∣∣2=2(|¯a|2+∣∣¯b∣∣2). परिणाम की ज्यामितीय व्याख्या कीजिए |07:37View Solutionकिन्हीं दो शून्येतर सदिशों के लिए, सिद्ध कीजिए कि
∣∣¯a+¯b∣∣=∣∣¯a−¯b∣∣⇔¯a⊥¯b. परिणाम की ज्यामितीय व्याख्या कीजिए |03:17View Solutionयदि ΔABC के शीर्षों के स्थिति सदिश ¯a,¯b,¯c हों, तो दर्शाइए कि उसका क्षेत्रफल
12(¯bׯc+¯cׯa+¯aׯb) है |
अत: निगमन कीजिए कि सदिशों ¯a,¯b,¯c के संरेख होने का प्रतिबन्ध है :
¯bׯc+¯cׯa+¯aׯb=¯0.05:32View Solutionकिन्ही दो सदिशों ¯a और ¯b के लिए, दर्शाइए कि
(1+|¯a|2)(1+∣∣¯b∣∣2)=(1−¯a⋅¯b)2+∣∣¯a+¯b+(¯aׯb)∣∣2.04:03View Solutionमान ज्ञात कीजिए : (¯a,¯b+¯c,¯a+¯b+¯c).
04:47View Solutionसदिश ¯a=α¯i+2¯j+β¯k, सदिशों ¯b=¯i+¯j तथा ¯c=¯j+¯k के तल में स्थित है तथा ¯b और ¯c के बीच के कोण का समद्विभाजन करता है, तो निम्न में से कौनसा α और β के सम्भावित मान प्रदान करता है ?
02:40View Solutionदर्शाइए कि दो शून्येतर सदिशों ¯a और ¯b के लिए,
|¯a|¯b+∣∣¯b∣∣¯a,|¯a|¯b−∣∣¯b∣∣¯a पर लम्ब है |03:05View Solutionयदि x2+(a−b)x+(1−a−b)=0, जहाँ a,b∈R, तो b के समस्त मानों के लिए, a के वे मान ज्ञात कीजिए, जिनके लिए समीकरण के असमान वास्तविक मूल होंगे|
02:55View Solutionबूलियन व्यंजक ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(A+B)+(A.B) = 1 के लिये A तथा B के निवेशी क्या होंगे
View Solution

