An element having atomic mass 63.1 g/mol has face centered cubic unit cell with edge length 3.608×10−8 cm. Calculate the density of unit cell [Given NA=6.022×1023 atoms/mol]. Solution in Kannada
(a) 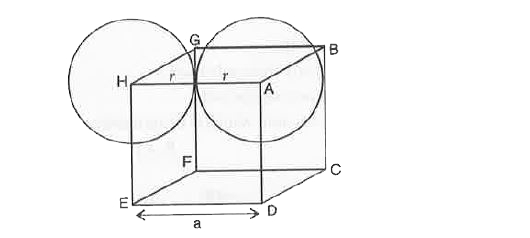
In simple cubic unit cell , the number of particle is one i.e., considered as one sphereThe volume of one particle (1 sphere)=42πr3Radius of each particle (sphere)=r⎫⎪
⎪⎬⎪
⎪⎭.....(i)
The volume of the unit cell = a3=(2r)3=8r3
Packing efficiency=Volume occupied by 1 spheresTotal volume of the unit cell×100
Or Z×Volume of a particleVolume of the unit cell×100
Packing efficiecy = 43πr38r3×100=52.4%
(b) d=ZMa3NA
d=4atoms×63.1g/mol(3.608×10−8cm)3×(6.022×1023)atoms/mol
d=8.92gcm−3.
Topper's Solved these Questions
- BOOK - OSWAAL PUBLICATIONCHAPTER - II PUC MARCH - 2017EXERCISE - PART - C8videos
II PUC MARCH - 2017
- BOOK - OSWAAL PUBLICATIONCHAPTER - II PUC APRIL - 2016 EXERCISE - PART - D27videos
II PUC APRIL - 2016
- BOOK - OSWAAL PUBLICATIONCHAPTER - II PUC MARCH - 2018EXERCISE - PART - D11videos
II PUC MARCH - 2018
Similar Questions
In the extraction of Aluminium by Hall- Herault process:
Give the equation of overall cell reaction.02:20View Solutiona) Calculate the packing efficiency of particles in a body centred cube.
03:45View SolutionAn element having atomic mass 107.9 u has FCC lattice. The edge length of its unit cell is 408.6 pm. Calculate density of the unit cell.
[Given, NA=6.022×1023mol−1].02:31View SolutionAn element with density 10 g cm^(-3) forms a cubic unit cell with edge length 3xx10^(-8)cm . What is the nature of the cubic unit cell if the atomic mass of the element is 81 g mol^(-1) .
01:21View SolutionAn element 'X' (At. Mass = 40 g mol−1) having f.c.c structure has unit cell edge length of 400 pm . Calculate the density of 'X' and the number of unit cells in 4 g of 'X' .
(NA=6.022×1023mol−1).02:33View SolutionAn element with density 11.2 g cm^(-3) forms a f.c.c lattic with edge lengh of 4 xx 10^(-8) cm. calculate the of atoms mass of the element ( Given : N_(A) = 6.022 xx 10^(23) mol^(-1)
01:21View SolutionAn element having atomic mass 63.1 g/mol has face centered cubic unit cell with edge length 3.608 xx 10^(-8) cm. Calculate the density of unit cell [Given N_(A) = 6.022 xx 10^(23) atoms/mol].
02:05View SolutionAn element has a body centered cubic structure with a unit cell edge length of 400 pm. Atomic mass of an element is 24 gmol^(-1) What is the density of the element? (N_A = 6 times 10^23 mol^-1)
03:10View SolutionAn element having atomic mass 63.1 g/mol has face centered cubic unit cell with edge length 3.608×10−8 cm. Calculate the density of unit cell [Given NA=6.022×1023 atoms/mol].
05:27View SolutionAn element having atomic mass 107.9 u had FCC lattice. The edge length of its unit cell is 408.6 pm. Calculate density of the unit cell. [Given , NA=6.022×1023].
03:51View SolutionAn element with density 11.2 g cm−3 forms a fcc lattice with edge length of 4×10−8 cm. Calculate the atomic mass of the element. (Given : NA=6.022×1023mol−1)
02:51View SolutionAn element 'X' (At. Mass = 40 g mol−1) having f.c.c structure has unit cell edge length of 400 pm . Calculate the density of 'X' and the number of unit cells in 4 g of 'X' .
(NA=6.022×1023mol−1).View SolutionCalcium metal crystallises in a face centered cubic lattice with edge length of 0.556nm. Calculate the density of the metal. [Atomic mass of calcium 40 g/mol] [N_(A) = 6.022 xx 10^(23) " atoms/ mol"]
06:26View SolutionAn element having atomic mass 63.1 g/mol has face centred cubic unit cell with edge length 3.608xx10^(-8)cm . Calculate the density of unit cell. [Given : NA=6.022xx1023" atoms/mol" ].
02:13View SolutionAn element (at. mass = 60) having face centred cubic unit cell has a density of 6.23g cm−3. What is the edge length of the unit cell? (Avogadro's constant = 6.023×1023mol−1)
04:04View Solution

