The function whose graph is the reflection about the line x+y=0 of the inverse function f−1 of a function f(x) is
Step by step video & image solution for The function whose graph is the reflection about the line x+y=0 of the inverse function f^(-1) of a function f(x) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Suppose f(x)=(x+1)2 for x≥−1. If g(x) is the function whose graph is the reflection of the graph of f (x) with respect to the line y = x, then g(x) equals
A−√x−1x≥0B1(x+1)2,x≥−1C√x+1,x≥−1D√x−1,x≥0 - Question 2 - Select One
If the graph of a function f(x is symmetrical about the line x = a, then
Af(a+x)=f(a−x)Bf(a+x)=f(x−a)Cf(x)=f(−x)Dnone of these - Question 3 - Select One
The graph of the function y=f(x) is symmetrical about the line x=2, then :
Af(x+2)=f(x−2)Bf(2+x)=f(2−x)Cf(x)=f(−x)Dnone of these
Consider the following function f, whose graph is given below.
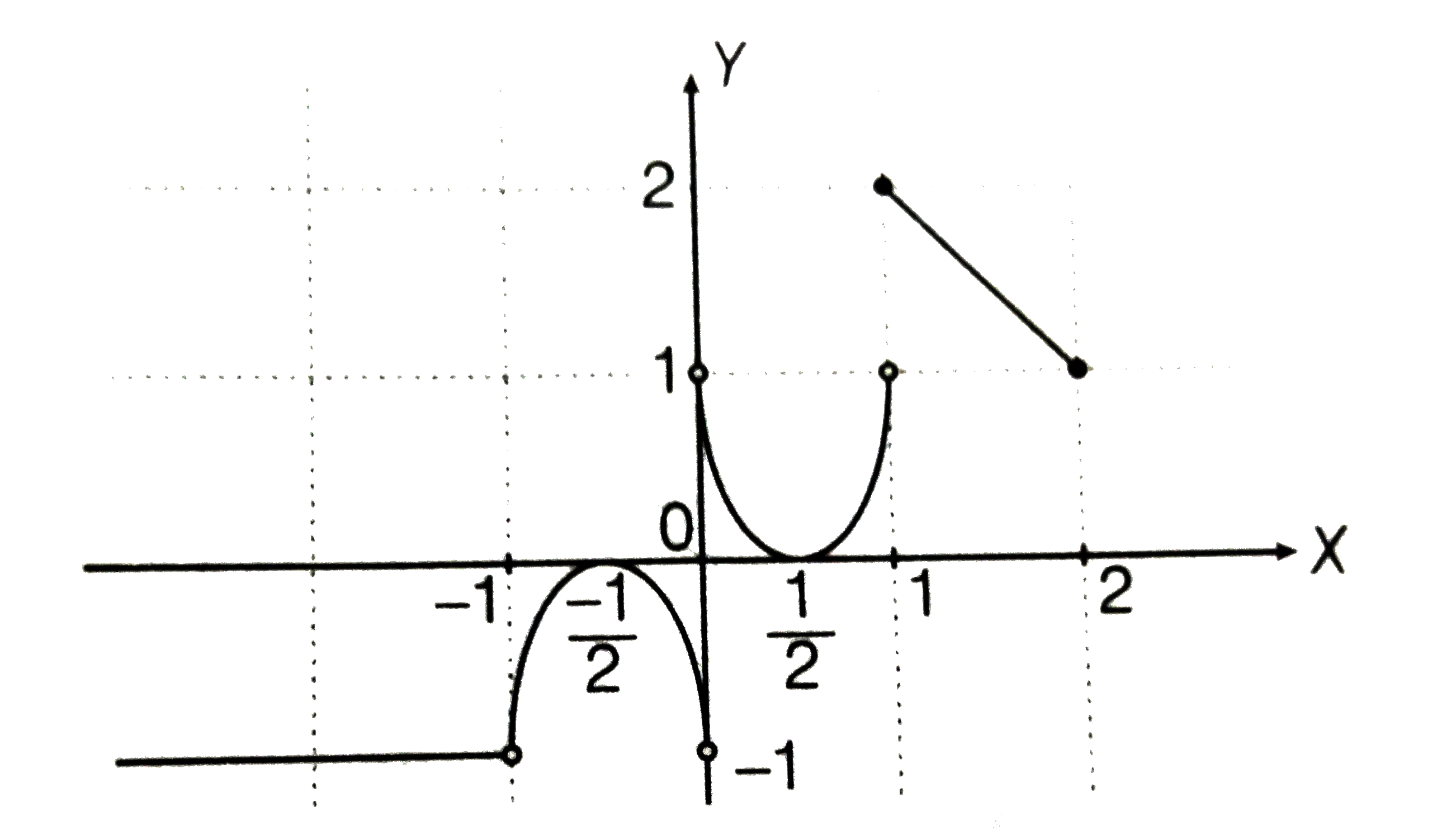
Draw the graph of the following functions.
(i) |f(x)|
(ii) f(|x|)
(iii) |f(|x|)−1|View SolutionIf the function f:R rarr R be such that f(x)=sin(tan^(-1)x) then inverse of the function f(x) is
View SolutionIf the function f:R rarr R be such that f(x)=sin(tan^(-1)x) then inverse of the function f(x) is
View SolutionIf the function f:R rarr R be such that f(x)=sin(tan^(-1)x) then inverse of the function f(x) is
View SolutionThe graph of the function y=f(x) is symmetrical about the line x=2, then :
View Solution
