ABCD is a quadrilateral in which ∠ABC=∠BCD and CD>AB Prove that ∠BAD>∠ADC
Step by step video & image solution for ABCD is a quadrilateral in which /_ABC=/_BCD and CD>AB Prove that /_BAD>/_ADC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the adjacent figure ABCD is a quadriateral & ∠ADB=∠BCA=22∘, then ∠BCD+∠BAD is-
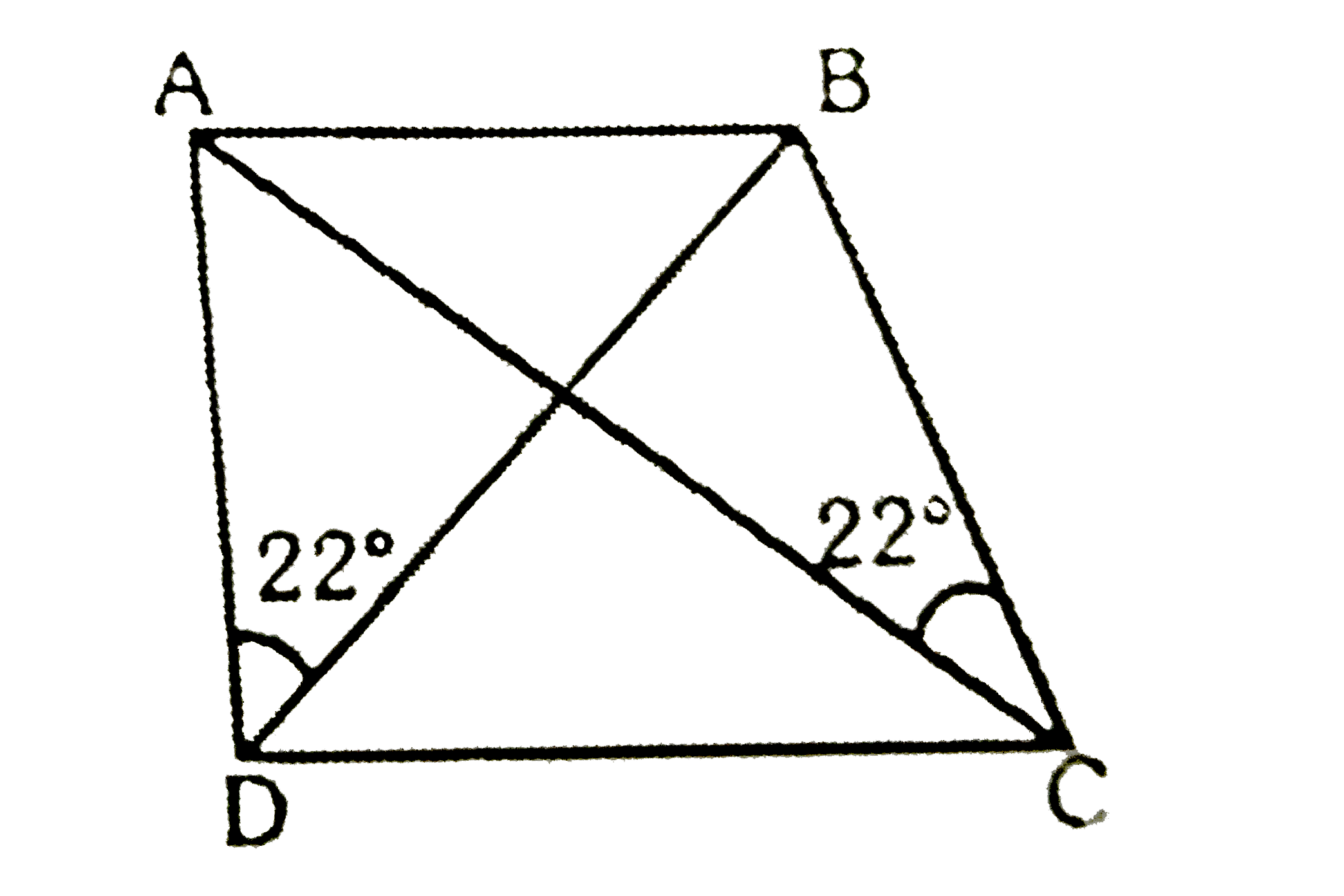 A66∘B90∘C132∘D180∘
A66∘B90∘C132∘D180∘
ABCD is a quadrilateral in which AB=BC and AD =CD ,Show that BD bisects boht the angle ABC and ADC
View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
View SolutionABCD is a quadrilateral in which AB=CD and AD=BC. show that it is a parallelogram.
View SolutionIn the adjacent figure ABCD is a quadriateral & ∠ADB=∠BCA=22∘, then ∠BCD+∠BAD is-

View SolutionABCD is a cyclic quadrilateral in which ∠BAD=750, ∠ABD=580and ∠ADC=770, AC and BD intersect at P. then, find ∠DPC
View Solutionsquare ABCD is a cyclic quadrilateral in which AB = AD .∠BCD=70∘ . Find (i) m (arc BCD) (ii) m (arc BAD) (III) ∠ADB
View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC bisects angle BAD
View Solution
