दो विभिन्न पदार्थों वाली छड़ों के रेखीय प्रसार गुणांक α1 व α2 तथा यंग गुणांक क्रमश: Y1 व Y2 हैं, इन्हें दो स्थिर दीवारों के बीच कसा गया है। छड़ों को इस प्रकार गर्म किया जाता है कि प्रत्येक के ताप में समान वृद्धि होती है, छड़ें झुकती नहीं हैं। यदि α1:α)2=2:3 एवं छड़ों के तापीय प्रतिबल बराबर हैं, तो Y1:Y2 का मान होगा
2:3
1:1
3:2
4:9
The correct Answer is:C
उष्मीय प्रतिबल के सूत्र से,
(FA)1=α1Y1ΔT ...(i)
(FA)2=α2Y2ΔT ...(ii)
(चूँकि ताप ΔT समान है)
∴(FA)1(FA)1=α1Y1α1Y2
उष्मीय प्रतिबल संतुलन हेतु,
α1Y1=α2Y2
याY1Y2=α2α1=32 (α1α2=2:3)
Topper's Solved these Questions
- ठोसों के गुणBOOK - ARIHANT HINDICHAPTER - ठोसों के गुणEXERCISE - प्रश्नावली (स्तर 2)
52 Videos
- ठोस एवं अर्ध्दचालक युक्तियाँ BOOK - ARIHANT HINDICHAPTER - ठोस एवं अर्ध्दचालक युक्तियाँ EXERCISE - प्रश्नावली स्तर 2 विगत वर्षों के प्रशन
9 Videos
- तरंग गति BOOK - ARIHANT HINDICHAPTER - तरंग गति EXERCISE - प्रारम्भिक प्रश्नावली 2
6 Videos
Similar Questions
चित्र में दिखाए गए स्टील तथा पीतल के तारों की लम्बाइयों, त्रिज्याओं तथा यंग प्रत्यास्थता गुणांकों में अनुपात क्रमशः a,b तथा c हैं। पीतल के तार की लम्बाई में वृद्धि तथा स्टील के तार की लम्बाई में वृद्धि में अनुपात होगा
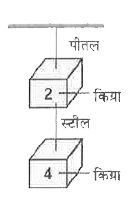
View SolutionOR गेट के निर्गत को NAND गेट के दोनों निवेशों से जोड़ा जाता है। संयोजन इस भाँति कार्य करेगा
View Solutionजब एक स्रोत ध्वनि के वेग से अधिक वेग से चलता है तो क्या डॉप्लर प्रभाव होगा?
View Solutionएक कम्पनी दो प्रकार के टेलीफ़ोन A व B बनाती है|A प्रकार के टेलीफ़ोन बनाने में 2 घण्टे एवं 300 टेलीफोनों को एक दिन में पैक किया जा सकता है| A प्रकार के टेलीफ़ोन का विक्रय मूल्य रु 300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य रु 400 है| अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफ़ोन का निर्माण करती है तो रेखीय प्रतिबन्ध (x≥0,y≥0 के अलावा ) है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न के रेखीय कार्य योजना का सम्भाव्य क्षेत्र के निम्न प्रकार का है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त क्षेत्र के शीर्ष है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न का अनुकूलतम है निम्नलिखित शीर्ष पर है|
View Solutionसिद्ध कीजिए की (1−4x)1/2 के प्रसार में xr का गुणांक
⌊2r⌊r⌊r है|
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
यदि B वर्ष 2010 तथा 2011 में कुल प्रदूषण 2.4 इकाई हो तो वर्ष 2008 व 2009 में प्रदूषण कितना मापा गया ?
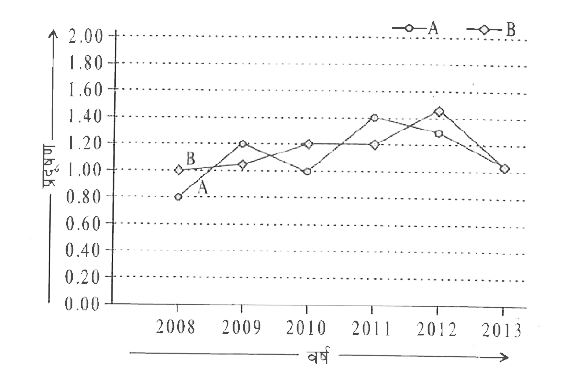
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
यदि B वर्ष 2010 तथा 2011 में कुल प्रदूषण 2.4 इकाई हो तो वर्ष 2008 व 2009 में प्रदूषण कितना मापा गया ?

View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solution(1−t61−t)3 के प्रसार में t4 का गुणांक है
View Solutionयदि (1+xlog2x)5 के द्विपद प्रसार में तीसरा पद 2560 के बराबर है, तो x का एक सम्भव मान है
View Solutionयदि , y1,y2 क्रमश: परवलय पर P व Q बिन्दुओं की कोटियाँ हैं, एवं y3 इन विन्दुओं पर खींची गयी स्पर्शियों के प्रतिच्छेद बिन्दु की कोटि है, तो
View Solutionयदि समीकरण (a2+4a+3)x2+(a2−a−2)x+a(a+1)=0 के दो से अधिक मूल हैं, तो a का मान है
View Solution