आकाश के किसी निश्चित क्षेत्र में विद्युत क्षेत्र सम्पूर्ण z-दिशा के अनुदिश है विद्युत क्षेत्र का परिमाण यद्यपि नियत नहीं है किन्तु 105N C−1 m−1 की दर से धनात्मक z-दिशा के अनुदिश एकसमान रूप से बढ़ता है ऋणात्मक z-दिशा में 10−7cm के बराबर कुल द्विध्रुव आघूर्ण वाले निकाय द्वारा अनुभव किया गया बल होगा -
−10−2N
10−2N
10−4N
−10−4N
The correct Answer is:A
माना कि A पर −q आवेश के साथ तथा B पर +q आवेश के साथ विद्युत द्विध्रुव z-अक्ष के अनुदिश स्थित है तो इसका द्विध्रुव आघूर्ण ऋणात्मक z दिशा में होता है
अर्थात pz=−10−7 cm
z-अक्ष की धनात्मक दिशा के अनुदिश विद्युत क्षेत्र है जैसे कि
dEdz=105 N C−1 m−1
F=qdE से
=(q×dz)×dEdz=pdEdz
∴F=10−7×105=−10−2N

Topper's Solved these Questions
- विद्युत आवेश तथा क्षेत्र BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युत आवेश तथा क्षेत्र EXERCISE - बहुविकल्प प्रश्न पिटारा (सतत् आवेश वितरण)
6 Videos
- विद्युत आवेश तथा क्षेत्र BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युत आवेश तथा क्षेत्र EXERCISE - बहुविकल्प प्रश्न पिटारा (गाउस का नियम)
5 Videos
- विद्युत आवेश तथा क्षेत्र BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युत आवेश तथा क्षेत्र EXERCISE - बहुविकल्प प्रश्न पिटारा (विद्युत द्विध्रुव)
6 Videos
- विकिरण तथा द्रव्य की द्वैत प्रकृति BOOK - NCERT FINGERTIPS HINDICHAPTER - विकिरण तथा द्रव्य की द्वैत प्रकृति EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- विद्युत धारा BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युत धारा EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
Similar Questions
निम्न का मिलान करे सही विकल्प का पता करें।
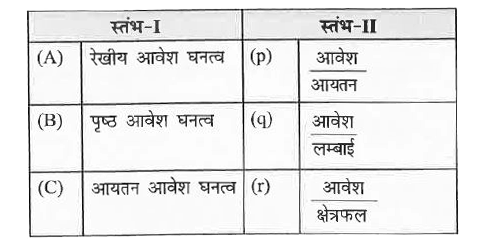
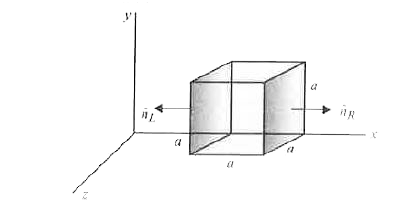
View Solutionदिये गये चित्र में विद्युत क्षेत्र घटक Ex=ax1/2,Ey=Ez=0 है जिसमे α=800 N C−1 m−1/2 है यदि घन में नेट फ्लक्स 1.05 N m2 C−1 है तो के अंदर आवेश क्या होगा ?
(=0.1m मानकर)
View Solutionएक गोला अपने अन्दर एक विद्युत द्विध्रुव को घेरे हुए है गोले का कुल फ्लक्स क्या होगा ?
View Solutionअभिकथन : किसी धातु के अंदर मुक्त इलेक्ट्रॉन धातु के बाहर घूमने के लिए स्वतंत्र होते है।
तर्क : चालक के अंदर मुक्त इलेक्ट्रॉनों को धातु के बाहर आने के लिए अतिरिक्त ऊर्जा की आवश्यकता नहीं होती है।
View Solutionअभिकथन: विद्युत वाहक बल एक ऐसा बल होता है जो इलेक्ट्रॉन के प्रवाह एवं धारा उत्पन्न करने में मदद करता है।
तर्कः विद्युत वाहक बल सेल में वोल्टता पर निर्भर नहीं करता है।
View Solution4×10−9Cm द्विध्रुव आघूर्ण का कोई विद्युत द्विध्रुव 5×104NC−1 परिमाण के किसी एकसमान विद्युत क्षेत्र की दिशा से 30∘ पर संरेखित है। द्विध्रुव पर कार्यरत बल आघूर्ण का परिमाण परिकलित कीजिये।
View Solutionएक वैद्युत तथा चुम्बकीय तरंग किसी माध्यम में वेग vecV = v, से जा रही है। वैद्युत-चुम्बकीय तरंग के वैद्युत दोलन Y-अक्ष के अनुदिश हैं। (i) चुम्बकीय क्षेत्र के दोलन किस दिशा में हो रहे होंगे ? (ii) वैद्युत क्षेत्र तथा चुम्बकीय क्षेत्र के परिमाण परस्पर किस प्रकार सम्बन्धित होंगे?
View Solutionविद्युत क्षेत्र का भौतिक अभिप्राय || बिंदु आवेश के कारण विद्युत् क्षेत्र || आवेशों के निकाय के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionवैद्युत क्षेत्र रेखाएँ || विद्युत क्षेत्र का भौतिक अभिप्राय || बिंदु आवेश के कारण विद्युत् क्षेत्र || आवेशों के निकाय के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionआवेशों के निकाय के कारण विद्युत क्षेत्र || वैद्युत द्विध्रुव तथा द्विध्रुव का आघूर्ण || वैद्युत द्विध्रुव के कारण क्षेत्र अक्षीय स्थिति में || कुछ प्रश्न
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionविद्युत क्षेत्र में द्विध्रुव को घुमाने में किया गया कार्य |खोखले या चालक गोले के कारण विद्युत विभव #!#संधारित्र
View Solutionद्विध्रुव के कारण विद्युत क्षेत्र
View Solutionकूलॉम के नियम पर महत्वपूर्ण उदाहरण |विद्युत क्षेत्र |विद्युत क्षेत्र की दिशा |विद्युत बल एवं विद्युत क्षेत्र मे संबंध | विद्युत क्षेत्र का अध्यारोपण |OMR|Summary
View Solutionप्रश्न |विद्युत क्षेत्र |बिन्दु आवेश के कारण विद्युत क्षेत्र की तीव्रता |विद्युत क्षेत्र की तीव्रता की गुण |प्रश्न |एक समरूप आवेशित वलय के कारण विद्युत क्षेत्र |OMR|Summary
View SolutionRevision|विद्युत द्विध्रुव के कारण सामान्य बिंदु पर विद्युत क्षेत्र|विद्युत द्विध्रुव के कारण विद्युत विभव|समरूप विद्युत क्षेत्र में विद्युत द्विध्रुव|चालक|OMR|Summary
View Solution
