△ABC এর ভিতরে P যেকোনো একটি বিন্দু | প্রমাণ করো যে, AB+BC+AC<2(AP+BP+CP)
Step by step video & image solution for triangleABC এর ভিতরে P যেকোনো একটি বিন্দু | প্রমাণ করো যে, AB+BC+AClt2(AP+BP+CP) by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- জ্যামিতিক প্রমানBOOK - NCERT BANGLISH (BANGLISH MEDIUM)CHAPTER - জ্যামিতিক প্রমানEXERCISE - EXERCISE
42 Videos
- ঘনফল নির্ণয়BOOK - NCERT BANGLISH (BANGLISH MEDIUM)CHAPTER - ঘনফল নির্ণয়EXERCISE - EXERCISE
55 Videos
- ত্রিভুজ অঙ্কনBOOK - NCERT BANGLISH (BANGLISH MEDIUM)CHAPTER - ত্রিভুজ অঙ্কনEXERCISE - EXERCISE
6 Videos
Similar Questions
বহুভুজটির অন্তঃকোনের সমষ্টি লেখো – পঞ্চভুজ
View Solutionঅভেদের সাহায্যে নীচের বীজগাণিতিক সংখ্যামালার ঘন নির্ণয় করো : 2y+3
View Solutionএকটি ত্রিভুজ আঁকো যার দুটি বাহুর দৈর্ঘ্য 5 সেমি ও 10 সেমি এবং 10 সেমি দৈর্ঘ্যের বাহুর বিপরীত কোণ 100^@ |
View SolutionIn Figure, P, is any point on the chord BC of a circle such that AB=AP. Prove that CP=CQ.
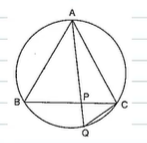
View SolutionIn ABC, ∠B=350,∠C=650 and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
View SolutionLet P be an interior point of a triangle ABC and AP, BP, CP meet the sides BC, CA, AB in D, E, F, respectively. Show that APPD=AFFB+AEEC.
View SolutionABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC और ∠B तथा ∠C के समद्विभाजक P पर प्रतिच्छेद करते हैं | साबित करें कि BP = CP और साथ ही AP,∠BAC का समद्विभाजक है |
View Solutionसंलग्न चित्र में , बिंदु P और Q,BC पर इस प्रकार है कि BQ = CP तथा AP = AQ तो दिखाइये कि AB = AC

View Solutionत्रिभुज ABC में,∠B=35∘,∠C=65∘ तथा ∠BAC का समद्विभाजक BC से P से पर मिलता है | AP,BP तथा CP को अवरोही क्रम में लिखिए |
View SolutionI is the incentre of the ΔABC. The perpendicular drawn from I to BC intersects BC at. P. Prove that AB−AC=BP−CP.
View SolutionIn a ΔABC, AB = 6, BC = 5 and CA = 4 and AP bisects the angle A. If P lies on BC then BP =
View Solutionx+y+1=0সরলরেখাস্থযেবিন্দু3x+4y +2 = 0-এর থেকে 1/5 একক দূরত্বে অবস্থিত সেই বিন্দুর স্থানাঙক হল—
View Solutionমনে করো xy সমতলে অবস্থিত S একটি বৃত্ত, যা x2+y2 = 4 সমীকরণ দ্বারা সংজ্ঞাত। মনে করো S বৃত্তের ওপর P এমন একটি বিন্দু যার স্থানাঙ্ক দুটি (x স্থানাঙ্ক ও yস্থানাঙ্ক) ধনাত্মক। মনে করো P বিন্দুতে S বৃত্তের স্পর্শক অক্ষদ্বয়কে M ও N বিন্দুতে ছেদ করেছে। তবে MN সরলরেখার মধ্যবিন্দু যে বক্রের ওপর অবস্থিত, তা হল—
View Solution△ABC -এর AD মধ্যমার উপর P একটি বিন্দু । বর্ধিত BP ও CP যথাক্রমে AC ও AB -কে Q ও R বিন্দুতে ছেদ করেছে । প্রমাণ করো যে, RQ∣∣BC
View Solution△ABC এর ভিতরে P যেকোনো একটি বিন্দু | প্রমাণ করো যে, AB+BC+AC<2(AP+BP+CP)
View SolutionIn a triangle ABC, BP is drawn perpendicular to BC to meet CA in P, such that CA = AP, then BPAB=
View Solution
