রজত একটি সরলরেখাংশ PQ অঙ্কন করেছে যার মধ্যবিন্দু R এবং সে PR ও PQ -কে ব্যাস করে দুটি বৃত্ত অঙ্কন করেছে । আমি P বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা প্রথম বৃত্তকে S বিন্দুতে এবং দ্বিতীয় বৃত্তকে T বিন্দুতে ছেদ করেছে । যুক্তি দিয়ে প্রমান করো যে, PS = ST
Step by step video & image solution for রজত একটি সরলরেখাংশ PQ অঙ্কন করেছে যার মধ্যবিন্দু R এবং সে PR ও PQ -কে ব্যাস করে দুটি বৃত্ত অঙ্কন করেছে । আমি P বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা প্রথম বৃত্তকে S বিন্দুতে এবং দ্বিতীয় বৃত্তকে T বিন্দুতে ছেদ করেছে । যুক্তি দিয়ে প্রমান করো যে, PS = ST by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- বৃওস্থ স্কোন সম্পর্কিত উপপাদ্যBOOK - NCERT BANGLISH (BANGLISH MEDIUM)CHAPTER - বৃওস্থ স্কোন সম্পর্কিত উপপাদ্যEXERCISE - EXERCISE
69 Videos
- বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যাBOOK - NCERT BANGLISH (BANGLISH MEDIUM)CHAPTER - বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যাEXERCISE - EXERCISE
31 Videos
- বৃত্তের স্পর্শক অঙ্কন BOOK - NCERT BANGLISH (BANGLISH MEDIUM)CHAPTER - বৃত্তের স্পর্শক অঙ্কন EXERCISE - EXERCISE
8 Videos
Similar Questions
ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB=AC , BC -এর যে পার্শ্বে △ABC অবস্থিত, সেই পার্শ্বেই △DBC এমনভাবে অঙ্কন করা হলো যাতে ∠BAC=2∠BDC হয়। প্রমান করি যে, A -কে কেন্দ্র করে AB ব্যাসার্ধ নিয়ে যে বৃত্ত অঙ্কন করা হবে তা D বিন্দু ওই বৃত্তের উপর অবস্থিত হবে ।
View Solutionআনোয়ারদের বাড়ির সামনে একটি নিরেট লোহার স্তম্ভ আছে যার নীচের অংশ লম্ব বৃত্তাকার চোঙ আকৃতির এবং উপরের অংশ শঙ্কু আকৃতির। এদের ভুমিতলের ব্যাসের দৈর্ঘ্য 20 সেমি., চোঙাকৃতি অংশের উচ্চতা 2.8 মিটার এবং শঙ্কু আকৃতি অংশের উচ্চতা 42 সেমি।। 1 ঘনসেমি. লোহার ওজন 7.5 গ্রাম হলে, লোহার স্তম্ভের ওজন কত হবে তা হিসাব করো।
View Solution2.8 সেমি. দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি বৃত্ত অঙ্কন করো । বৃত্তের কেন্দ্র থেকে 7.5 সেমি. দূরে একটি বিন্দু নাও । ওই বহিঃস্থ বিন্দু থেকে বৃত্তের স্পর্শক অঙ্কন করো ।
View SolutionIn Figure, PQ=PR . Show that PS>PQ
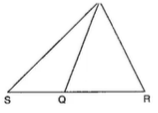
View SolutionIn Figure, PQ=PR. Show that PS>PQ
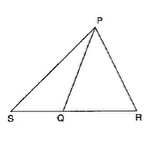
View SolutionIn ΔPQR,Pq=PR and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
View Solutionयदि रेखा PQ, PR, PS तथा PT रेखा l के समांतर है तो सिद्ध कीजिए बिन्दु P, Q, R, S तथा T संरेखीय है।
View Solutionआकृति में PR = PQ तो सिद्ध करें की PS>PQ
View SolutionIn figure ∠QPC=90∘, PS is its bisector. If ST⊥PR, prove that ST×(PQ+PR)=PQ×PR.
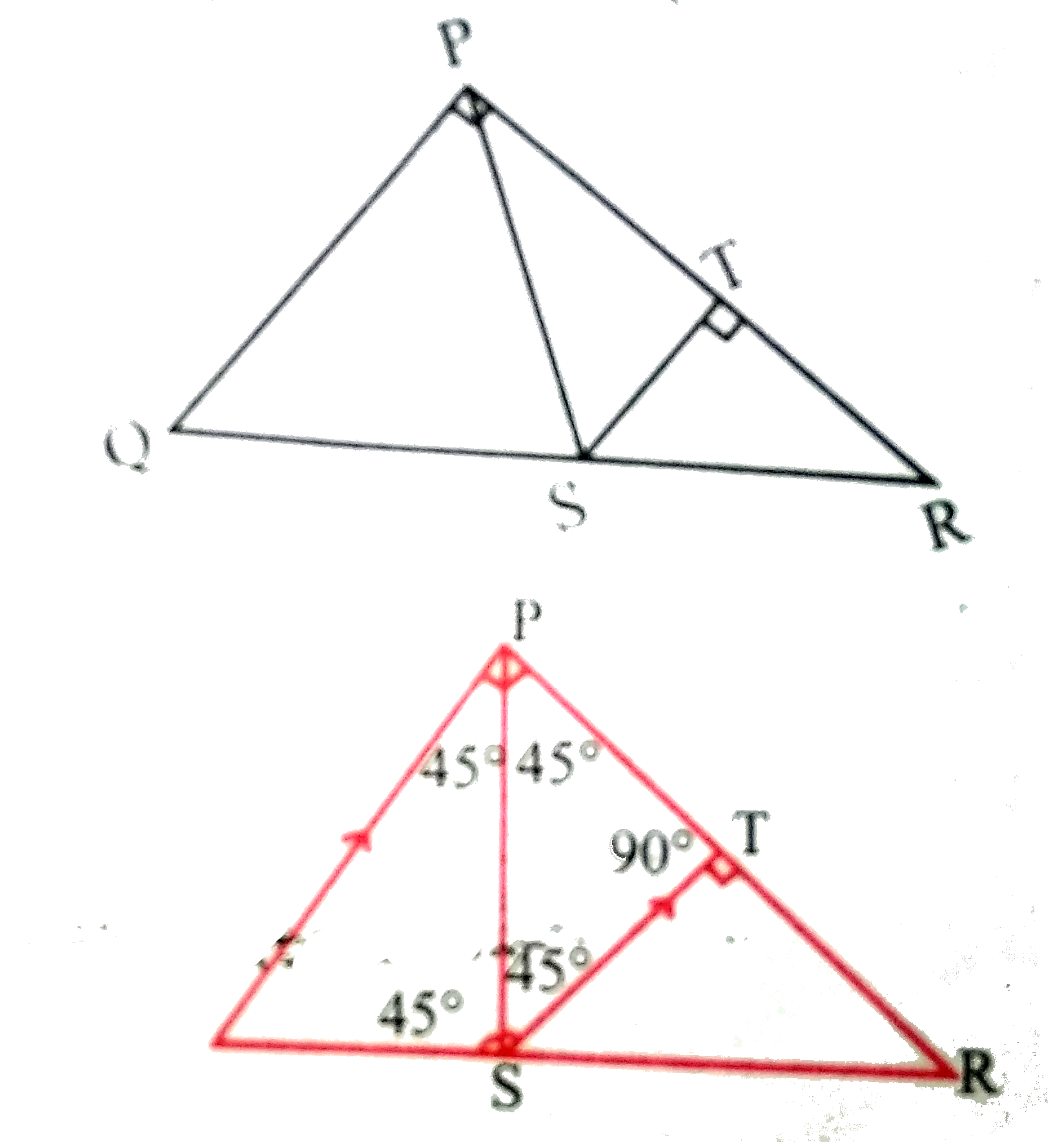
View Solutionমনে করো, Z=−1+√3i2,যেখানেi=sqrt-1এবংr,s,in{1,2,3}।P=[[(-z)^r,(z^2)^s],[(z^2)^s,z^r]]এবংIএকটি2ক্রমেরএককম্যাট্রিক্স।যতগুলিক্রমিকজোড়(r,s)−এরজন্যP^=-I হবে,তাহল-
View Solutionf(x)=x2−1x−1অপেক্ষকেরলেখচিত্রঅঙ্কনকরােএবংx = 1ওx= 2 বিন্দুতে অপেক্ষক সন্তত কি না তা লেখচিত্র থেকে বলাে।
View Solutionএকটি অপেক্ষক f(x)-এর নিম্নরূপ সংজ্ঞা দেওয়া হয় । f(x)={(x−1","যখন x>0),(−12","যখনx=0),(x+1","যখনx<0):}f(x)অপেক্ষকেরলেখচিত্রঅঙ্কনকরাে।লেখচিত্রথেকেf(x)অপেক্ষকেরx =-1/2বিন্দুতেমাননির্ণয়করােএবংx = 0বিন্দুতেf(x) সন্তত কি না বলে।
View Solutionসিম অপেক্ষক F(x) -এর সংজ্ঞা নীচে দেওয়া হল:F(x)={(1,,যখন x>0),(0,","যখনx=0),(−1,,যখন x<0):}অপেক্ষকের লেখচিত্র অঙ্কন করো এবং এর সংজ্ঞা অঞ্চল ওপাল্লা নির্ণয় করাে।
View Solution[θ=srঅথবা কণ (বৃত্তীয় মানে )=(চাপ)/(ব্যাসার্ধ),সূত্র−সম্পর্কিতপেশ্নাবলি।]দুটিবৃত্তএমনযে,একটিঅপরটিকেন্দ্রবিন্দুগামী।প্রথমবৃত্তেরlদৈর্ঘ্যেরচাপতারকেন্দ্রেthetaএবংদ্বিতীয়বৃত্তেরmদৈর্ঘ্যেরচাপতারকেন্দ্রেphiসম্মুখকোণউৎপন্নকরে।প্রমাণকরােযে,lphi=mtheta।
View Solutionমনে করো xy সমতলে অবস্থিত S একটি বৃত্ত, যা x2+y2 = 4 সমীকরণ দ্বারা সংজ্ঞাত। মনে করো S বৃত্তের ওপর P এমন একটি বিন্দু যার স্থানাঙ্ক দুটি (x স্থানাঙ্ক ও yস্থানাঙ্ক) ধনাত্মক। মনে করো P বিন্দুতে S বৃত্তের স্পর্শক অক্ষদ্বয়কে M ও N বিন্দুতে ছেদ করেছে। তবে MN সরলরেখার মধ্যবিন্দু যে বক্রের ওপর অবস্থিত, তা হল—
View Solutionপ্রতিটি প্রশ্নে বিবৃতি-1 এবং বিবৃতি-2 দেওয়া আছে। প্রতিটি প্রশ্নের বিবৃতি দুটি নীচের কোন বিকল্পটিকে (A, B, C ও D-এর মধ্যে) সঠিকভাবে ব্যাখ্যা করে? সরলরেখা l:→r=ˆi−ˆj+ˆk+t(2ˆi+3ˆj−6ˆk) এবং সমতল p:→r.(2ˆi+3ˆj−6ˆk)=7। বিবৃতি−1সরলরেখাlসমতলp−কেএকটিঅনন্য(unique)বিন্দুতেছেদকরে।বিবৃতি−2l সরলরেখা p সমতলের ওপর লম্ব।
View Solution
