△ABC ও △DBC সদৃশকোণী। অতএব তারা
সর্বসম
সদৃশ
সদৃশ নয়
সর্বসম নয়
The correct Answer is:B
Step by step video & image solution for triangleABC ও triangleDBC সদৃশকোণী। অতএব তারা by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
△ABC -এর BC -এর সমান্তরাল সরলরেখা AB ও AC -কে যথাক্রমে D ও E বিন্দুতে ছেদ করলে প্রমাণ করো যে,ABDB=ACEC
View Solutionআমি একটি মুখবন্ধ লম্ব বৃত্তাকার শঙ্কু তৈরি করেছি যার ভুমির ব্যাসার্ধের দৈর্ঘ্য 15 সেমি এবং তির্যক উচ্চতা 24 সেমি| ওই শঙ্কুর পার্শ্ব তলের ক্ষেত্রফল ও সমগ্রতলের ক্ষেত্রফল হিসাব করে লেখো|
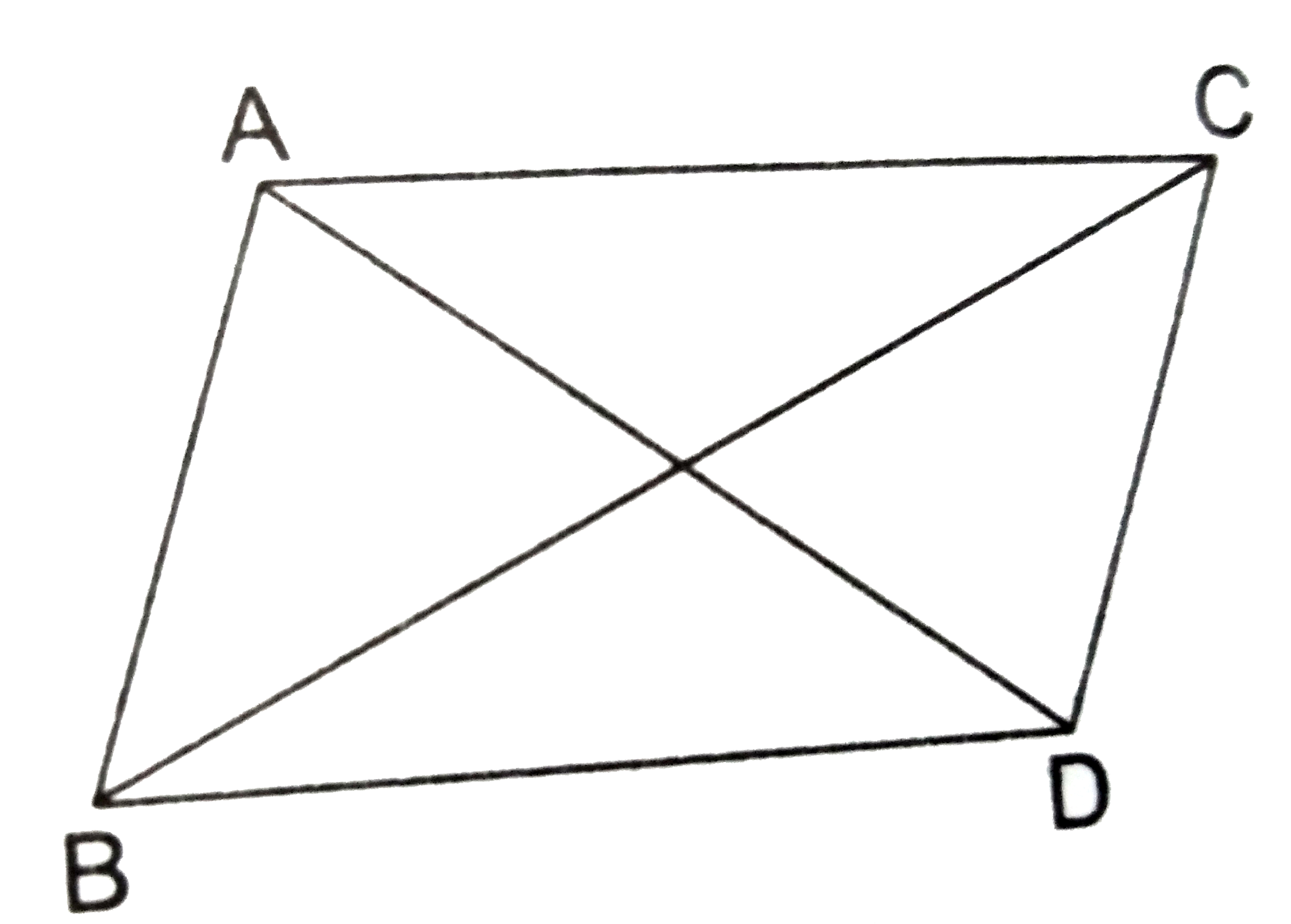
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
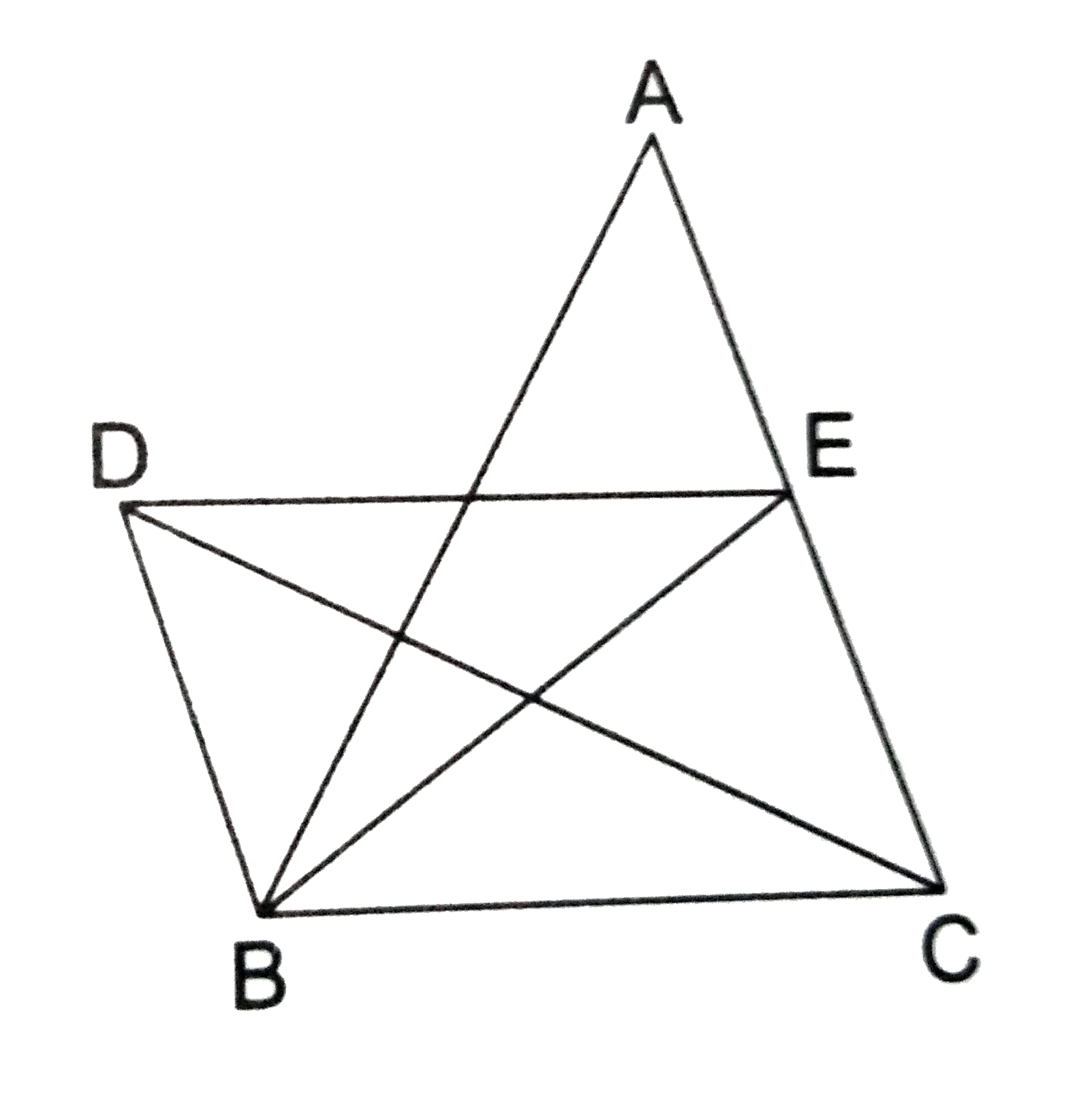
View SolutionIn the adjoining figure, BD||CA, E is the midpoint of CA and BD=12CA. Prove that
ar(△ABC)=2ar(△DBC).
View Solutionबिंदुओं A,B,C तथा D के निर्देशांक क्रमशः (6,3),(−3,5),(4,−2) तथा (x,y) है तो सिद्ध कीजिए कि △DBC△ABC=|x+y−2|7
View Solutionयदि किसी △ABC में, b,c और A दिए हुए है, तो △ABC का क्षेत्रफल है
View Solutionयदि किसी △ABC में, △ABC की परित्रिज्या R हो और △ABC का क्षेत्रफल △ है, तो
View Solutionचित्र 8 में, एक ही आधार BC पर तथा विपरीत दिशाओं में दो त्रिभुज △ABC तथा △DBC बने हुए हैं तथा AD और BC का प्रतिच्छेदन बिन्दु O है। सिद्ध कीजिए कि क्षेत्रफल (△ABC) क्षेत्रफल (△DBC)=AODO

View SolutionIn △ABC, if a=13,b=14,c=15, then A(△ABC)=
View SolutionIn △ABC, if a=18,b=24,c=30, then A(△ABC)
View SolutionIn a △ABC, if cosAa=cosBb=cosCc then △ABC is
View Solution△ABCஇல்
View SolutionABC একটি সমদ্বিবাহু ত্রিভুজ যার AB=AC , BC -এর যে পার্শ্বে △ABC অবস্থিত, সেই পার্শ্বেই △DBC এমনভাবে অঙ্কন করা হলো যাতে ∠BAC=2∠BDC হয়। প্রমান করি যে, A -কে কেন্দ্র করে AB ব্যাসার্ধ নিয়ে যে বৃত্ত অঙ্কন করা হবে তা D বিন্দু ওই বৃত্তের উপর অবস্থিত হবে ।
View SolutionUse the information given in the adjoining figure, to prove △DBC≅△EAC
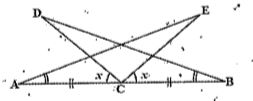
View Solution
