A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
What is the magnitude of the normal force exerted on the block by the hoop when the block has reached the bottom ?
mg
3mg
mg2R
2mg
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Initial Conditions
A block of mass m is released from rest at a height R above the bottom of a circular hoop of radius R. The acceleration due to gravity is g.
Step 2: Apply Conservation of Energy
At the initial height R, the block has potential energy and no kinetic energy since it is at rest. When it reaches the bottom of the hoop, all potential energy will have converted into kinetic energy.
- Potential Energy at height R:
PEA=mgh=mgR
- Kinetic Energy at the bottom:
KEB=12mv2
By conservation of energy:
PEA=KEB
Thus,
mgR=12mv2
Step 3: Solve for Velocity v
We can cancel m from both sides (assuming m≠0):
gR=12v2
Multiplying both sides by 2:
2gR=v2
Taking the square root:
v=√2gR
Step 4: Analyze Forces at the Bottom of the Hoop
At the bottom of the hoop, the block experiences two forces:
1. The gravitational force mg acting downward.
2. The normal force N exerted by the hoop acting upward.
For the block to maintain circular motion, the net force towards the center of the circle must equal the required centripetal force. The centripetal force Fc is given by:
Fc=mv2R
Step 5: Set Up the Equation for Forces
At the bottom of the hoop:
N−mg=mv2R
Step 6: Substitute for v2
From Step 3, we have v2=2gR. Substituting this into the force equation:
N−mg=m(2gR)R
This simplifies to:
N−mg=2mg
Step 7: Solve for Normal Force N
Rearranging the equation gives:
N=2mg+mg=3mg
Conclusion
The magnitude of the normal force exerted on the block by the hoop when the block has reached the bottom is:
3mg
---
A block of mass m is released from rest at a height R above the bottom of a circular hoop of radius R. The acceleration due to gravity is g.
At the initial height R, the block has potential energy and no kinetic energy since it is at rest. When it reaches the bottom of the hoop, all potential energy will have converted into kinetic energy.
PEA=mgh=mgR
- Kinetic Energy at the bottom:
KEB=12mv2
PEA=KEB
Thus,
mgR=12mv2
We can cancel m from both sides (assuming m≠0):
gR=12v2
Multiplying both sides by 2:
2gR=v2
Taking the square root:
v=√2gR
At the bottom of the hoop, the block experiences two forces:
1. The gravitational force mg acting downward.
2. The normal force N exerted by the hoop acting upward.
Fc=mv2R
At the bottom of the hoop:
N−mg=mv2R
From Step 3, we have v2=2gR. Substituting this into the force equation:
N−mg=m(2gR)R
This simplifies to:
N−mg=2mg
Rearranging the equation gives:
N=2mg+mg=3mg
The magnitude of the normal force exerted on the block by the hoop when the block has reached the bottom is:
3mg
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Matrix-Match)1videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)10videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)4videos
WAVES-I
Similar Questions

A block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given above. What force is exerted by the rope on the block ?View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope , the force exerted by the rope on the block .
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
Which one of the following expressions gives the speed of the mass at the bottom of the hoop ?Azerom/s2Bv=mg2RCv2=2gRDv=mgR - Question 2 - Select One
Two forces act on a 4.5 kg block resting on a frictionless surface as shown in the given figure. What is the magnitude of the horizontal acceleration of the block ?
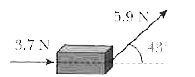 A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2
A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2 - Question 3 - Select One
A block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given. What force is exerted by the rope on the block ?
 AF3BF2C2F3DF
AF3BF2C2F3DF
Block of mass m is stationary w.r.t. wedge. Normal force exerted by wedge on the block is
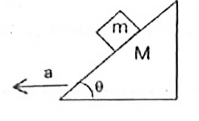 View Solution
View SolutionA block of mass m is released from a height R on the frictionless incline as shown. The incline leads to a circle of radius R/2. The maximum height attained by the block is
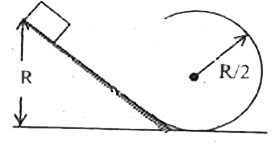 View Solution
View SolutionA 10 kg block is connected to a 40 kg block as shown in the figure. The surface on that the blocks slide is frictionless. A force of 50 N pulls the blocks to the right.

What is the magnitude of the acceleration of the 40 kg block ?View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block is
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block is
View Solution

