वक्तव्य I यदि दीर्घवृत x2a2+y2b2=1,(a>b) के बिंदु P (प्रथम चतुर्थांश में) पर खींची गई स्पर्श रेखा, संगत नियता x=a/e के बिंदु Q, पर मिलती है तब जीवा PQ वाला निम्नतम क्षेत्रफल का वृत्त, दीर्घवृत की नाभि से होकर जाता है।
वक्तव्य II PQ, संगत नाभि पर समकोण आंतरित करता है।
वक्तव्य I सत्य है वक्तव्य II भी सत्य है वक्तव्य II, वक्तव्य I का सही स्पष्टीकरण है।
वक्तव्य I सत्य है वक्तव्य II भी सत्य है वक्तव्य II, वक्तव्य I का सही स्पष्टीकरण नहीं है।
वक्तव्य I सत्य है, वक्तव्य II असत्य है।
वक्तव्य I असत्य है, वक्तव्य II सत्य है
The correct Answer is:A
Topper's Solved these Questions
- दीर्घवृतBOOK - ARIHANT HINDICHAPTER - दीर्घवृतEXERCISE - प्रश्नावली स्तर 2 (विगत वर्षों के प्रश्न)
7 Videos
- दीर्घवृतBOOK - ARIHANT HINDICHAPTER - दीर्घवृतEXERCISE - प्रश्नावली स्तर 2 (श्रृंखलाबद्ध बोधन प्रकार)
3 Videos
- त्रिविमीय ज्यामिति का परिचयBOOK - ARIHANT HINDICHAPTER - त्रिविमीय ज्यामिति का परिचयEXERCISE - प्रश्नावली
32 Videos
- दीर्घवृत्तBOOK - ARIHANT HINDICHAPTER - दीर्घवृत्तEXERCISE - प्रश्नावली (लक्ष्य JEE Main) (विगत वर्षो के प्रश्न )
8 Videos
Similar Questions
दीर्घवृत x216+y29=1 की नाभि से होकर जाने वाले तथा (0,3) केंद्रक वाले वृत्त का समीकरण है
View Solutionदीर्घवृत x2a2+y2b2=1 इस प्रकार है कि इसका क्षेत्रफल निम्नतम लेकिन वृत्त (x−1)2+y2=1 को समाहित करता है।
दीर्घवृत की उत्केंद्रता है
View SolutionXy- समतल से समांत समतल लंब होगा
View Solutionवृत्त (x−1)+y2=1 के व्यास को अर्द्ध लघु अक्ष लेकर तथा वृत्तx2+(y−2)2=4 के एक व्यास को अर्द्ध दीर्घ अक्ष लेकर एक दीर्घवृत्त खींचा गया। यदि दीर्घवृत्त का केन्द्र मूलबिन्दु पर है तथा अक्ष निर्देशांक अक्ष हैं, तो दीर्घवृत्त का समीकरण है
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionरेखा y=x+a√2 वृत्त को x2+y2=a2 बिंदु …………. पर स्पर्श करता है ।
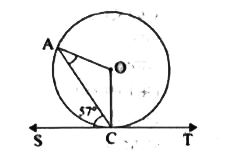
View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
View Solutionयदि किसी बिंदु P के परवलय y2=4x पर खींची गई दो स्पर्श-रेखाएँ परस्पर लम्ब हों, तो P का बिन्दुपथ है :
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solutionयदि वृत्त x2+y+6x+6y=2 के बिन्दु P पर खींची गई स्पर्शी सरल रेखा 5x−2y+6=0 से y-अक्ष के बिन्दु Q पर मिलती है, तो PQ की लम्बाई है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionवृत्त x2+y2=4 के बिंदु (√3,1) पर खींची गई स्पर्श रेखा और अभिलम्ब तथा X-अक्ष एक त्रिभुज बनाते है । इस त्रिभुज का (वर्ग इकाइयो में) क्षेत्रफल है
View Solutionयदि बिंदु (4,6) से होकर जाने वाले मानक अतिपरवलय की उत्केंद्रता 2 है, तो (4,6) पर अतिपरवलय पर खींची गई स्पर्श रेखा का समीकरण है
View Solutionयदि वृत्त x2+y2=1 की एक स्पर्श रेखा निर्देशांक अक्षो को भिन्न बिन्दुओ P और Q पर प्रतिच्छेद करती है, तो PQ के मध्य -बिंदु का बिन्दुपथ (locus) है
View Solutionदीर्घवृत्त 3x2+5y2=32 के बिंदु P (2,2) पर खींची गई स्पर्श रेखा तथा अभिलम्ब, X-अक्ष को क्रमश: Q तथा R पर काटते है, तो ΔPQR का क्षेत्रफल (वर्ग इकाइयो में) है
View Solution
