AB is a chord of the circle x2+y2=252 .P is a point such that PA = 4, PB = 3. If AB = 5, then distance of P from origin can be:
Step by step video & image solution for AB is a chord of the circle x^2 + y^2 = 25/2 .P is a point such that PA = 4, PB = 3. If AB = 5, then distance of P from origin can be: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A variable line through A(6, 8) meets the circle x2+y2=2 at B and C. P is a point on BC such that AB, AP, AC are in H.P. Then the minimum distance of the origin from locus of P is
View SolutionAB is a chord of the circle x2+y2=25. The tangents of A and B intersect at C. If (2, 3) is the mid-point of AB,then area of the quadrilateral OACB is
View Solution
Knowledge Check
- Question 1 - Select One
AB is a chord of the circle x2+y2=25. The tangents of A and B intersect at C. If (2, 3) is the mid-point of AB,then area of the quadrilateral OACB is
A50√133B50√313C50√3D50√3 - Question 2 - Select One
Let AB and CD are two parallel chords of circle whose radius is 5 units. If P and Q are mid points of AB and CD respectively such that PA. PB = 9, QC. QD = 16, then distance between AB and CD is
A5B25C7D11
AB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionAB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionP(3,2)" is a point on the circle "x2+y2=13" .Two points "A" ,"B" are on the circle such that PA=PB=√5 .The equation of chord "AB" is
View SolutionIn the figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion.
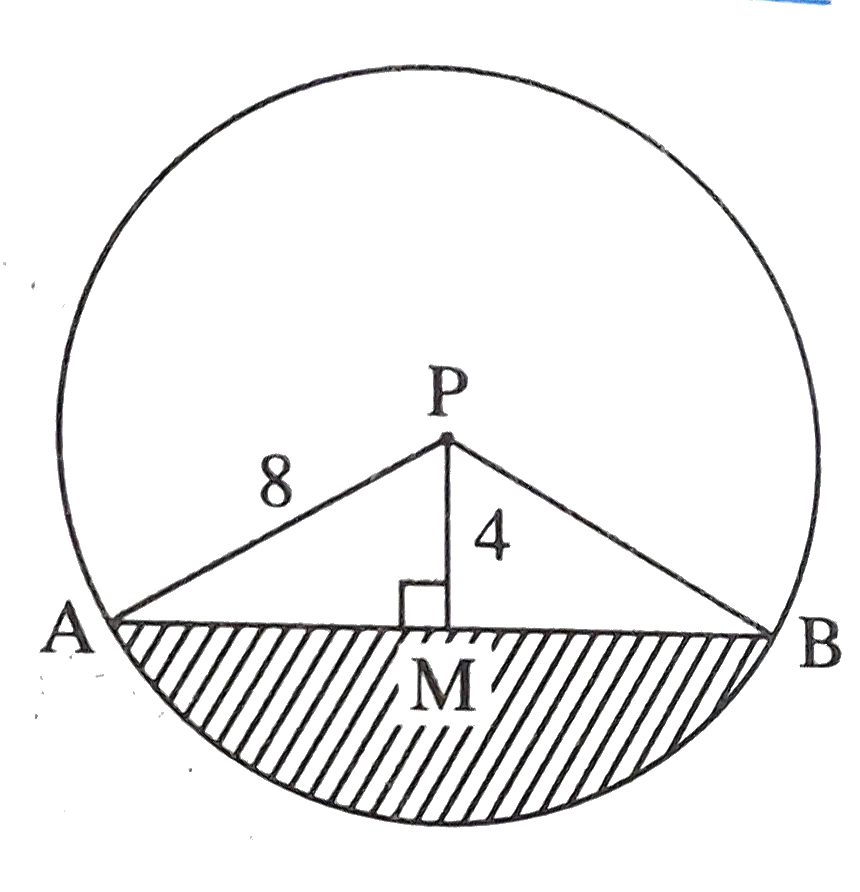 View Solution
View SolutionTangents are drawn from P(3,0) to the circle x2+y2=1 touches the circle at points A and B. The equation of locus of the point whose distances from the point P and the line AB are equal is
View SolutionA variable chord of the circle x2+y2=4 is drawn from the point P(3,5) meeting the circle at the point A and B. A point Q is taken on the chord such that 2PQ=PA+PB . The locus of Q is x2+y2+3x+4y=0 x2+y2=36 x2+y2=16 x2+y2−3x−5y=0
View Solution
