D, E and F are respectively the mid-points of the sides AB, BC and CA of a ΔABC. Prove that by joining these mid-points D, E and F, the ΔABC is divided into four congruent trianglesSolution in Kannada
The correct Answer is:ΔDEF≅ΔEDB≅ΔCFE≅ΔFAD
Step by step video, text & image solution for D, E and F are respectively the mid-points of the sides AB, BC and CA of a ΔABC. Prove that by joining these mid-points D, E and F, the ΔABC is divided into four congruent triangles by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:OSWAAL PUBLICATIONChapter:TRIANGLESExercise:TEXTBOOK CORNER (EXERCISE 2.5)
Explore 17 Videos
- TRIANGLESBook:OSWAAL PUBLICATIONChapter:TRIANGLESExercise:TEXTBOOK CORNER (EXERCISE 2.6)
Explore 10 Videos
- TRIANGLESBook:OSWAAL PUBLICATIONChapter:TRIANGLESExercise:TEXTBOOK CORNER (EXERCISE 2.3)
Explore 16 Videos
- SURFACE AREA AND VOLUMESBook:OSWAAL PUBLICATIONChapter:SURFACE AREA AND VOLUMESExercise:EXERCISE 15.5
Explore 5 Videos
Similar Questions
Sides of triangles are given below. Determine which of them are right triangles.
In case of a right triangle , write the length of its hypotenuse.
7cm, 24 cm, 25 cm
View SolutionIn the figure given below, PS is the bisector of ∠QPR of ΔPQR . Prove that QSSR=PQPR

View SolutionState which pairs of triangles in Fig are similar. Write the similarity criterion used by you for answering the question also write the pairs of similar triangles in the symbolic form:
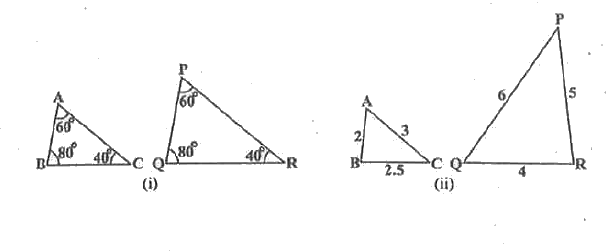
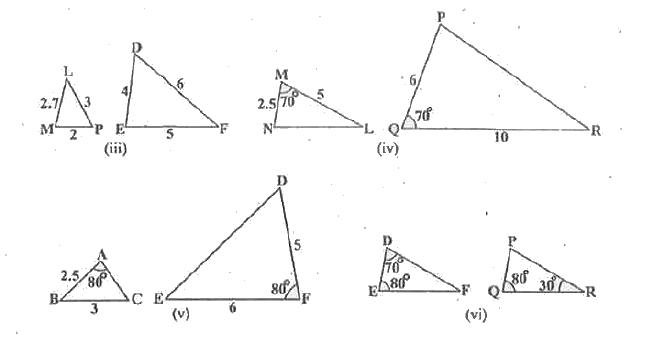
View SolutionA copper wire, 3mm in diameter , is wound about a cylinder whose length is 12cm, and diameter 10cm, so as to cover the curved surface of the cylinder . Find the length and mass of the wire, assuming the density of copper to be 8.88gpercm3
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionΔABC में ,D ,E और F क्रमश : भुजाओं AB , BC और CA में मध्य - बिंदु है ( देखिए आक्रति 8.27) | दर्शाइए कि बिन्दुओ D ,E और F को मिलाने पर ΔABC चार सर्वांगसम त्रिभुजों में विभाजित हो जाता है ।

View SolutionD, E and F are the mid-points of the sides AB, BC and CA of the ΔABC. Prove that ΔDEF=14ΔABC.
View SolutionABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View SolutionIn ΔABC , D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABC is divided into four congruent triangles by joining D, E and F.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. triangle DEF is congruent to triangle :
View SolutionIf D,E,F are the mid-point of sides AB,BC and CA respectively of △then the ratio of the areas of triangles △DEF and ABC is
View SolutionD, E and F are the mid-points of the sides AB, BC and CA of an isosceles triangle ABC in which AB = BC. Prove that ΔDEF is also isosceles.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View Solution