Circles C(O, r) and C(O', r'), (r>r') touch internally at P. PQ is a chord of circle C(O, r) which intersects C(O', r') at R. Show that OO'RQ is a trapezium
Step by step video & image solution for Circles C(O, r) and C(O', r'), (r gt r') touch internally at P. PQ is a chord of circle C(O, r) which intersects C(O', r') at R. Show that OO'RQ is a trapezium by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
In Figure, circle C(O,r)andC(O′r2) touch internally at a point. AandAB is a chord of the circle C(O,r) intersecting C(O′,r2) at C . Prove that AC=CB
View SolutionTwo circles C(O, r) and C'(O', r') touch externally at P(3, 1). If the co-ordinates of O and O' are (1, p) and (q, -2) repectively. Their areas are in the ratio 4 : 9. Find the value of p2+q2.
View Solution
Knowledge Check
Circles C(o, r) and C(O1,r2) touch internally at a point A and AB is a chord of the circle intersecting C(O1,r2) at C. Then AC is equal to :
ACBBOACOBD13 ABTwo circles of same radius r centred at O and O' touch each other at P as shown in the figure, if OO' is produced to meet the circle C(O'r) at A and AT is a tangent to the circle C(O,r) such that O'Q ⊥ AT . Then AO : AO'=
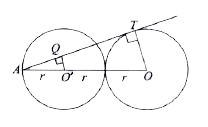 A32B2C3D14
A32B2C3D14Circles C1 and C2 of radii r and R respectively, touch each other as shown in the figure. The lime l, which is parallel to the line joining the centres of C2 and C2 is tangent to C1 at P and intersects C2 at A,B.If R2=2r2, then ∠AOB equals-
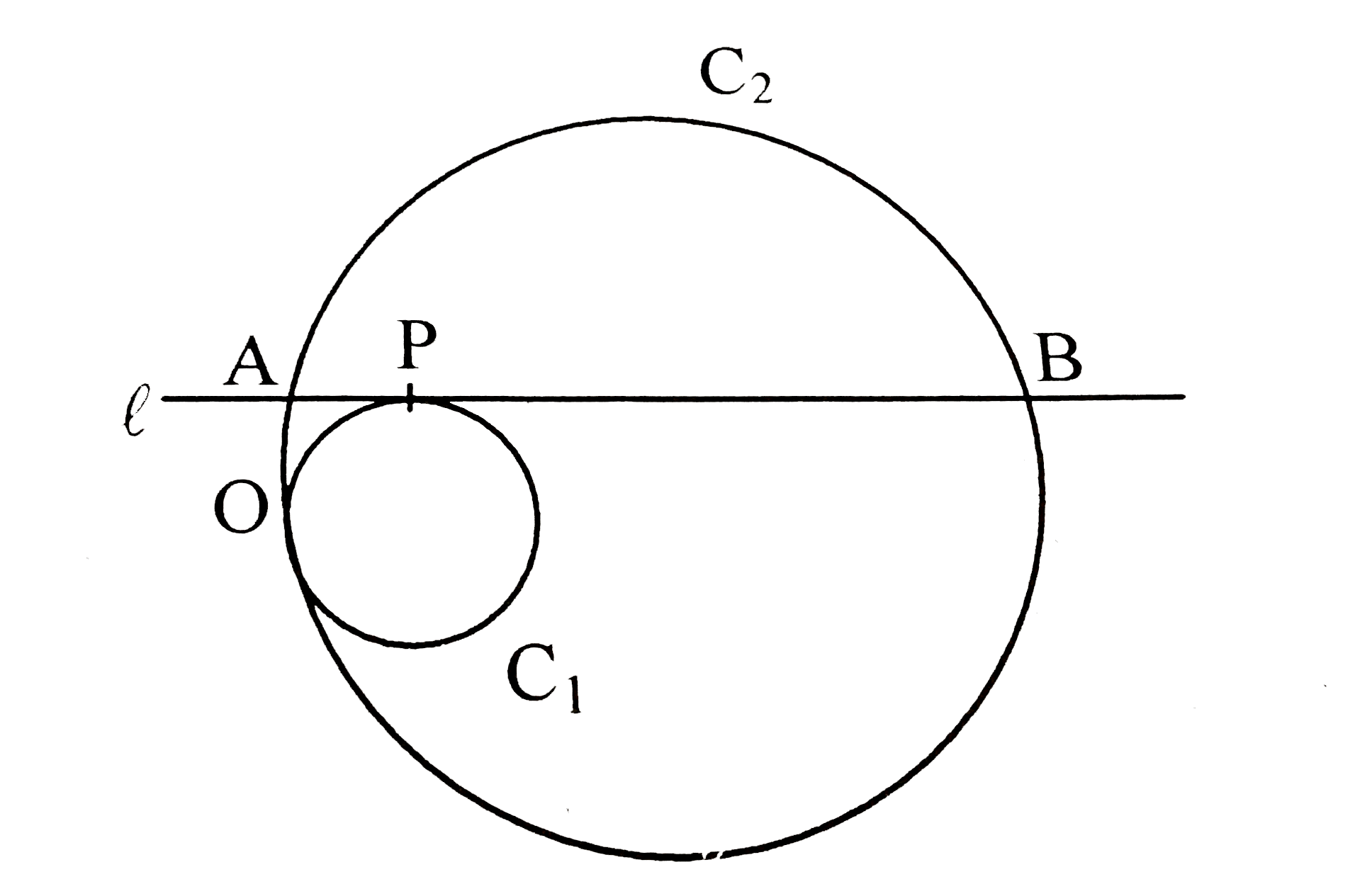 A2212∘B45∘C60∘D6712∘
A2212∘B45∘C60∘D6712∘
Two circles C(0, r) and C(O', r') touch extemally. Show that the length of a common tangent (not through the point of contact of the circles) is 2√rr'
View Solution) and In this figure two bigger circles C(0,r) and C(O',r') touch each other. On third circle C(0, r) are touching the two bigger circles as well as the common tangent. Then prove
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(△AOD)=ar(△BOC) . Prove that ABCD is a trapezium.
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View Solution
