Let g:R→R be a function such that, g(x)=2x+5. Then, what is g−1(x) equal to ?
x−52
2x-5
x−52
x2+52
The correct Answer is:A
To find the inverse of the function g(x)=2x+5, we will follow these steps:
Step 1: Set the function equal to y
Let y=g(x). Therefore, we have:
y=2x+5
Step 2: Solve for x in terms of y
To find the inverse function, we need to express x in terms of y. Start by isolating x:
y−5=2x
Now, divide both sides by 2:
x=y−52
Step 3: Write the inverse function
Now that we have x in terms of y, we can express the inverse function g−1(x) by replacing y with x:
g−1(x)=x−52
Final Answer
Thus, the inverse function is:
g−1(x)=x−52
---
Let y=g(x). Therefore, we have:
y=2x+5
To find the inverse function, we need to express x in terms of y. Start by isolating x:
y−5=2x
Now, divide both sides by 2:
x=y−52
Now that we have x in terms of y, we can express the inverse function g−1(x) by replacing y with x:
g−1(x)=x−52
Thus, the inverse function is:
g−1(x)=x−52
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let f:R→R,g:R→R be two functions such that
f(x)=2x−3,g(x)=x3+5 The function (fog)−1(x) is equal toA(x+72)13B(x−72)13C(x−27)13D(x−72)13Let f:R→R,g:R→R be two functions given by f(x)=2x−3,g(x)=x3+5. Then (fog)−1 is equal to
Ax+71/32Bx−71/22Cx−21/37Dx−71/32Let g (x) be a function such that g(x+1)+g(x−1)=g(x) for every real x. Then for what value of p is the relation g(x+p)=−g(x) necessarily true for every real x?
A5B3C2D6
Let f:R→R,g:R→R be two functions given by f(x)=2x−3,g(x)=x3+5. Then (fog)−1 is equal to
View SolutionLet f:R→R,g:R→R be two functions given by f(x)=2x−3,g(x)=x3+5. Then (fog)−1 is equal to
View SolutionA function f(x)=log(g(x)), where g(x) is any function of x.
If g(x)=ex. Then f(f(x)) is equal to :
View SolutionLet g(x)=1+x-[x] and
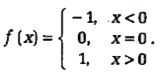 Then for all x,f {g(x)} is equal to
Then for all x,f {g(x)} is equal to
View SolutionLet f(x),g(x) be two real valued functions then the function h(x)=2max{f(x)−g(x),0} is equal to :
View Solution
