Let f be a function from the set of natural numbers to the set of even natural numbers given by f(x)=2x. Then f is
one to one but not onto
onto but not one-one
both one-one and onto
neither one-one nor onto
The correct Answer is:C

For each element in the domain there is only one element in the therefore f(x) is one-one.
No image in the co-domian which has no pre-image in the domian, therefore f(x) is onto
Hence f(x) both is one-one and onto.
Topper's Solved these Questions
Similar Questions
Let f be a one - to - one function from the set of natural number to itself such that f(mn) = f(m) f (n) for all natural numbers m and n. What is the least possible value f (999) ?
View SolutionLet f be a function from be set of positive integers to the set of real numbers i.e. f:N→R, such that
f(1)+2f(2)+3f(3)+……+nf(n)=n(n+1)f(n) form ge2, then find the value of f(1994).
View Solution
Knowledge Check
If f be a function from the set of natural numbers to the set of even natural numbers given by f(x) = 2x. Then, f is:
AOne-one but not ontoBOnto but not one-oneCBoth one-one and ontoDNeither one-one nor ontoA functions from the set of natural numbers to integers defined by
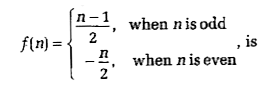 Aone-one but not ontoBonto but not one-oneCone-one and onto bothDnone of these
Aone-one but not ontoBonto but not one-oneCone-one and onto bothDnone of theseThe function f:N→N,N being the set of of natural numbers, defined by f(x)=2x+3 is
Ainjective and surjectiveBinjective but not surjectiveCnot injective but surjectiveDneither injective nor surjective
Let f be a function from C (set of all complex numbers) to itself given by f(x)=x3 . Write f−1(1) .
View SolutionThe function f:N→N,N being the set of of natural numbers, defined by f(x)=2x+3 is
View SolutionThe function f N → N. where N being the set of natural numbers, defined by f(x) = 2x + 3 is:
View SolutionThe function f:N→N (N is the set of natural numbers defined by f(n)=2n+3 is :
View SolutionThe function f:N→N (N is the set of natural numbers defined by f(n)=2n+3 is :
View Solution
