Question

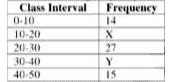
Consider the following frequency destribution :
$\begin{array}{cccccc}\text{Class interval}& 0-10& 10-20& 20-30& 30-40& 40-50\\ \text{Frequency}& 14& x& 27& y& 15\end{array}$
If the total of the frequencies is 100 and mode is 25, then which one of the following is correct?

Options

A. x = 2y
B. 2x = y
C. x = y
D. x = 3y

Answer

C

Explanation

To solve the problem, we need to analyze the given frequency distribution and the conditions provided.

Given:
- Class intervals: 0-10, 10-20, 20-30, 30-40, 40-50
- Frequencies: 14, x, 27, y, 15
- Total frequency = 100
- Mode = 25

Step 1: Set up the equation for total frequency
The total frequency can be expressed as:
\( 14 + x + 27 + y + 15 = 100 \)

Step 2: Simplify the equation
Combine the known frequencies:
\( 14 + 27 + 15 = 56 \)
Thus, the equation becomes:
\( 56 + x + y = 100 \)

Step 3: Solve for x + y
Rearranging gives:
\( x + y = 100 - 56 \)
\( x + y = 44 \)

Step 4: Determine the modal class
Given that the mode is 25, we need to identify the modal class. The modal class is the class interval with the highest frequency. The frequency for the class intervals is:
- 0-10: 14
- 10-20: x
- 20-30: 27
- 30-40: y
- 40-50: 15

Since the mode is 25, the modal class must be 20-30 (as it contains the value 25).

Step 5: Analyze the frequencies
For the modal class (20-30) to be the mode, it must have the highest frequency compared to the other class intervals. Therefore:
\( 27 > x \quad \text{(since 27 is the frequency for 20-30)} \)
\( 27 > y \quad \text{(since y is the frequency for 30-40)} \)

Step 6: Check the options
We need to check the relationships between x and y based on the equation \( x + y = 44 \) and the conditions \( x < 27 \) and \( y < 27 \).

1. Option A: \( x = 2y \)
- Substitute: \( 2y + y = 44 \) → \( 3y = 44 \) → \( y = \frac{44}{3} \) (not an integer)

2. Option B: \( x = y \)
- Substitute: \( y + y = 44 \) → \( 2y = 44 \) → \( y = 22 \), \( x = 22 \) (valid)

3. Option C: \( x = 3y \)
- Substitute: \( 3y + y = 44 \) → \( 4y = 44 \) → \( y = 11 \), \( x = 33 \) (not valid as \( x \) exceeds 27)

Conclusion
The only valid option is:
- Option B: \( x = y \), where both \( x \) and \( y \) equal 22.

Final Answer
Thus, the correct relationship is \( x = y \).